Cho hàm số \(y=f(x)\) có đồ thị \(f'(x)\) như hình vẽ.
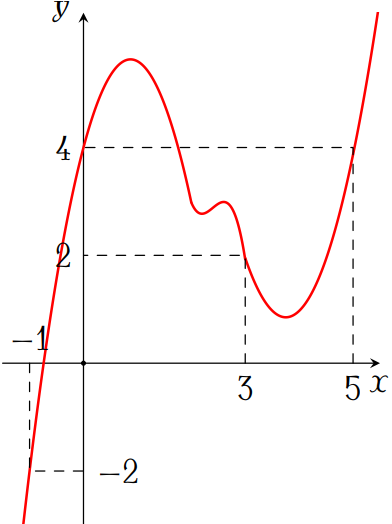
Đặt \(g(x)=2f(x)-(x-1)^2\). Mệnh đề nào dưới đây đúng?
| \(g(-1)< g(5)< g(3)\) | |
| \(g(3)< g(5)< g(-1)\) | |
| \(g(5)< g(-1)< g(3)\) | |
| \(g(-1)< g(3)< g(5)\) |
Chọn phương án A.
\(g'(x)=2f'(x)-2(x-1)=2\left[f'(x)-(x-1)\right]\).
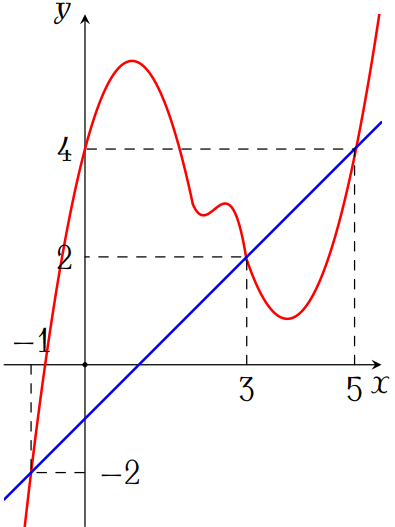
- Gọi \(S_1\) là diện tích hình phẳng giới hạn bởi đồ thị \(f'(x)\) và đường thẳng \(y=x-1\), đường thẳng \(x=-1\), \(x=3\).
- Gọi \(S_2\) là diện tích hình phẳng giới hạn bởi đồ thị \(f'(x)\) và đường thẳng \(y=x-1\), đường thẳng \(x=3\), \(x=5\).
$$\begin{aligned}
S_1&=\displaystyle\int\limits_{-1}^{3}\left[f'(x)-(x-1)\right]\mathrm{\,d}x\\
\Leftrightarrow2S_1&=\displaystyle\int\limits_{-1}^{3}2\left[f'(x)-(x-1)\right]\mathrm{\,d}x=\displaystyle\int\limits_{-1}^{3}g'(x)\mathrm{\,d}x\\
&=g(3)-g(-1)
\end{aligned}$$
Vì \(2S_1>0\) nên \(g(3)-g(1)>0\) hay \(g(3)>g(1)\).
$$\begin{aligned}
S_2&=\displaystyle\int\limits_{3}^{5}\left[(x-1)-f'(x)\right]\mathrm{\,d}x\\
\Leftrightarrow2S_2&=-\displaystyle\int\limits_{3}^{5}2\left[f'(x)-(x-1)\right]\mathrm{\,d}x=-\displaystyle\int\limits_{3}^{5}g'(x)\mathrm{\,d}x\\
&=g(3)-g(5)
\end{aligned}$$
Vì \(2S_2>0\) nên \(g(3)-g(5)>0\) hay \(g(3)>g(5)\).
Mặt khác, dựa vào đồ thị ta thấy $$\begin{eqnarray*}
&S_1&>S_2\\
\Leftrightarrow&2S_1&>2S_2\\
\Leftrightarrow&g(3)-g(-1)&>g(3)-g(5)\\
\Leftrightarrow&g(-1)&<g(5)
\end{eqnarray*}$$
Vậy \(g(-1)< g(5)< g(3)\).
