Ngân hàng bài tập
A
Cho hàm số \(y=ax^3+bx^2+cx+d\) (\(a,\,b,\,c,\,d\in\mathbb{R}\)) có đồ thị là đường cong trong hình.
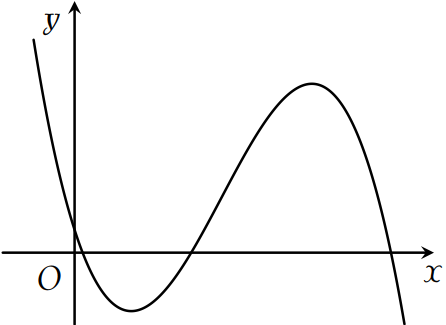
Có bao nhiêu số dương trong các số \(a\), \(b\), \(c\), \(d\)?
| \(4\) | |
| \(1\) | |
| \(2\) | |
| \(3\) |
1 lời giải
Chọn phương án C.
Dựa vào đồ thị ta thấy \(a<0\).
Vì hai điểm cực trị của đồ thị có hoành độ dương nên phương trình \(y'=3ax^2+2bx+c=0\) có
- \(x_1+x_2=-\dfrac{2b}{3a}>0\Rightarrow b>0\).
- \(x_1\cdot x_2=\dfrac{c}{3a}>0\Rightarrow c<0\)
Mặt khác, vì đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên \(d>0\).
Vậy có \(2\) số dương là \(b\) và \(d\).
