Cho hàm số bậc ba \(y=f(x)\) có đồ thị là đường cong trong hình.
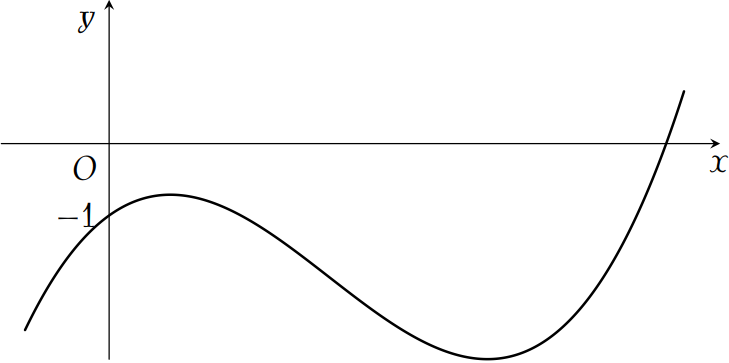
Số nghiệm thực phân biệt của phương trình \(f\left(x^3f(x)\right)+1=0\) là
| \(8\) | |
| \(5\) | |
| \(6\) | |
| \(4\) |
Chọn phương án C.
\(\begin{aligned}
f\left(x^3f(x)\right)+1=0\Leftrightarrow&f\left(x^3f(x)\right)=-1\\ \Leftrightarrow&\left[\begin{array}{l}
x^3f(x)=0\\
x^3f(x)=a>0\\
x^3f(x)=b>a
\end{array}\right.\\
\Leftrightarrow&\left[\begin{array}{ll}
x^3=0\\
f(x)=0 &(1)\\
f(x)=\dfrac{a}{x^3} &(2)\\
f(x)=\dfrac{b}{x^3} &(3)
\end{array}\right.
\end{aligned}\)
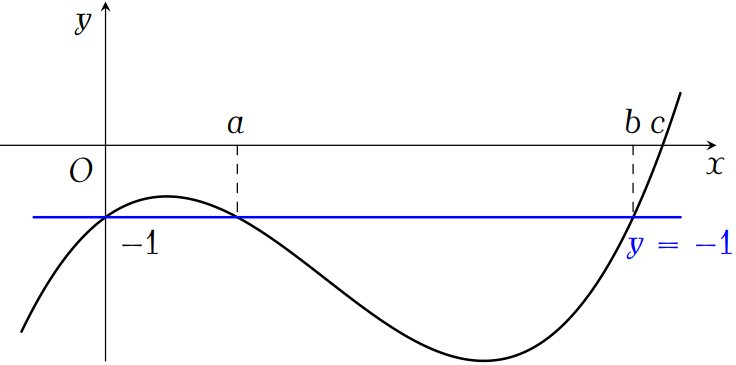
\(\blacksquare\) Phương trình (1) có một nghiệm \(x=c\).
\(\blacksquare\) Số nghiệm của phương trình (2) chính là số giao điểm của đồ thị \(f(x)\) với đồ thị hàm số \(g(x)=\dfrac{a}{x^3}\).
Vì \(a>0\) nên \(g'(x)=-\dfrac{3a}{x^4}<0\), \(\forall x\neq0\).
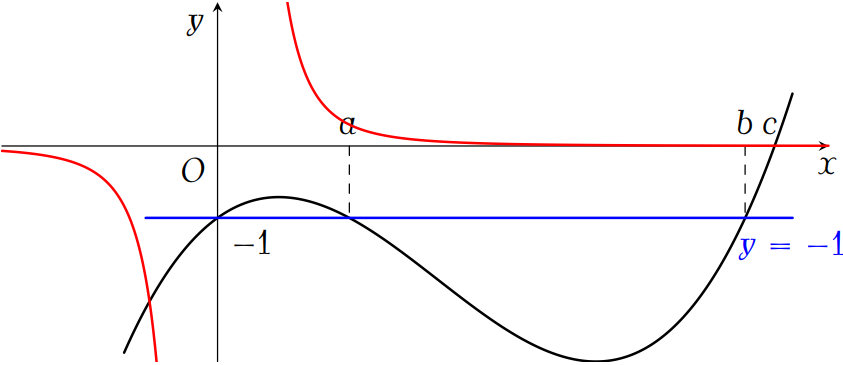
Ta thấy đồ thị \(f(x)\) và \(g(x)\) cắt nhau tại hai điểm là \(x=a_1<0\) và \(x=a_2>c\).
\(\blacksquare\) Số nghiệm của phương trình (3) chính là số giao điểm của đồ thị \(f(x)\) với đồ thị hàm số \(h(x)=\dfrac{b}{x^3}\).
Vì \(b>0\) nên \(h'(x)=-\dfrac{3b}{x^4}<0\), \(\forall x\neq0\).
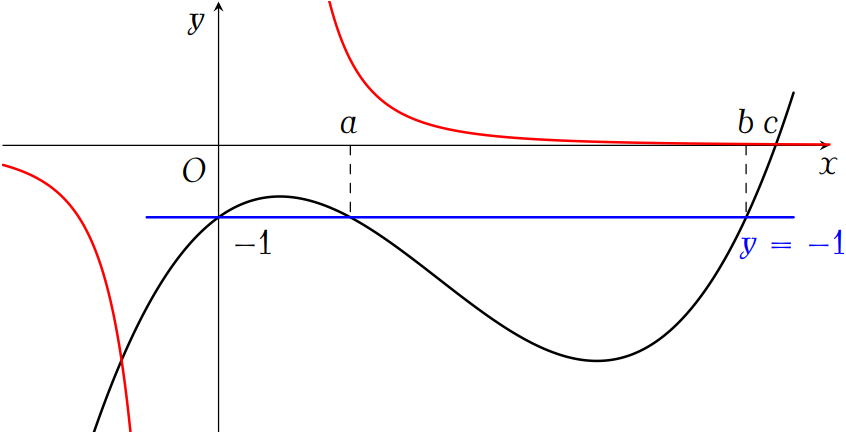
Ta thấy đồ thị \(f(x)\) và \(h(x)\) cắt nhau tại hai điểm là \(x=b_1<0\) và \(x=b_2>c\).
Vậy phương trình \(f\left(x^3f(x)\right)+1=0\) có đúng \(6\) nghiệm.
