Cho hàm số bậc bốn \(f\left(x\right)\) có bảng biến thiên như sau: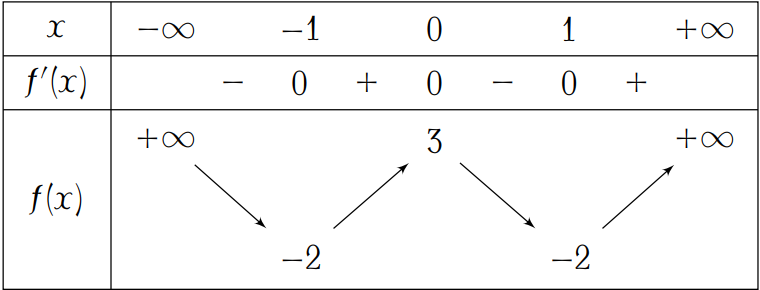
Số điểm cực trị của hàm số \(g\left(x\right)=x^4\left[f\left(x+1\right)\right]^2\) là
| \(11\) | |
| \(9\) | |
| \(7\) | |
| \(5\) |
Chọn phương án B.
Theo bảng biến thiên ta thấy $$f\left(x\right)=5x^4-10x^2+3$$Suy ra \(f'(x)=20x^3-20x\).
Khi đó $$\begin{aligned}g'\left(x\right)&=4x^3\left[f\left(x+1\right)\right]^2+2x^4f\left(x+1\right)f'\left(x+1\right)\\ &=2x^3f\left(x+1\right)\left[2f\left(x+1\right)+xf'\left(x+1\right)\right]\end{aligned}$$
\(\begin{aligned}
\text{Cho }g'\left(x\right)=0\Leftrightarrow&\left[\begin{array}{l}
x^3=0\\
f\left(x+1\right)=0\\
2f\left(x+1\right)+xf'\left(x+1\right)=0
\end{array}\right.\\
\Leftrightarrow&\left[\begin{array}{ll}
x^3=0 &(1)\\
f\left(x+1\right)=0 &(2)\\
2f\left(x+1\right)+xf'\left(x+1\right)=0 &(3)
\end{array}\right.
\end{aligned}\)
\(\blacksquare\) Phương trình (1) có một nghiệm bội ba \(x=0\) nên là một điểm cực trị của \(g(x)\).
\(\blacksquare\) Theo bảng biến thiên ta thấy phương trình \(f\left(x\right)=0\) có \(4\) nghiệm đơn phân biệt khác \(0\) nên (2) cũng có \(4\) nghiệm đơn phân biệt khác \(0\). Vậy cả \(4\) nghiệm này cũng là điểm cực trị của \(g(x)\).
\(\blacksquare\) Số nghiệm của phương trình (3) trùng với số nghiệm của phương trình $$\begin{eqnarray*}
&2f\left(x\right)+(x-1)f'\left(x\right)&=0\\
\Leftrightarrow&2\left(5x^4-10x^2+3\right)+(x-1)\left(20x^3-20x\right)&=0\\
\Leftrightarrow&10x^4-20x^2+6+20x^4-20x^2-20x^3+20x&=0\\
\Leftrightarrow&15x^4-10x^3-20x^2+10x+3&=0.
\end{eqnarray*}$$Dễ thấy phương trình này có \(4\) nghiệm đơn phân biệt.
Vậy số điểm cực trị của hàm số \(g\left(x\right)\) là \(9\).
