Ngân hàng bài tập
C
Giá trị nhỏ nhất của hàm số \(f\left(x\right)=x^3-24x\) trên đoạn \(\left[2;19\right]\) bằng
| \(32\sqrt{2}\) | |
| \(-40\) | |
| \(-32\sqrt{2}\) | |
| \(-45\) |
2 lời giải
Chọn phương án C.
Dùng chức năng TABLE trên máy tính cầm tay.
- Nhập \(f(x)=x^3-24x\).
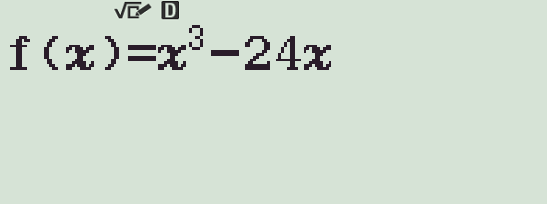
- Chọn Start, End và Step
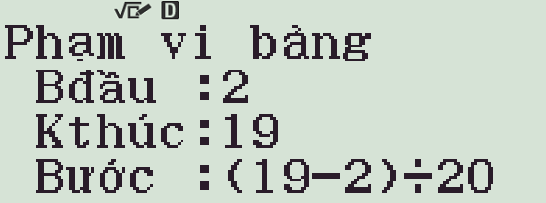
- Quan sát bảng giá trị ta thấy giá trị nhỏ nhất gần bằng với \(-32\sqrt{2}\)
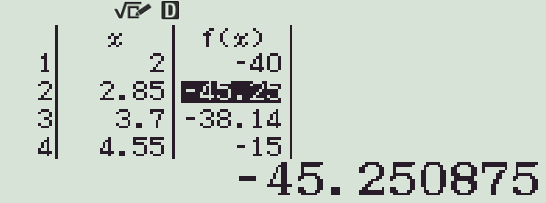
Chọn phương án C.
Ta có \(f'\left(x\right)=3x^2-24\).
Cho \(f'\left(x\right)=0\Leftrightarrow\left[\begin{array}{ll}x=2\sqrt{2} &\in\left[2;19\right]\\ x=-2\sqrt{2} &\notin\left[2;19\right].\end{array}\right.\)
Ta có \(f\left(2\right)=-40\), \(f\left(2\sqrt{2}\right)=-32\sqrt{2}\), \(f\left(19\right)=6403\).
Vậy giá trị nhỏ nhất của hàm số \(f\left(x\right)=x^3-24x\) trên đoạn \(\left[2;19\right]\) là \(-32\sqrt{2}\).
