Ngân hàng bài tập
C
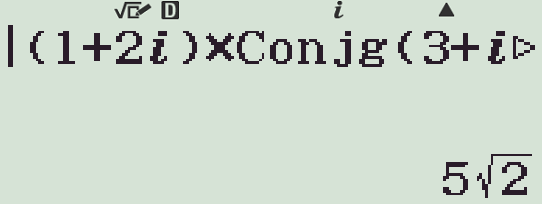
Cho hai số phức \(z=1+2i\) và \(w=3+i\). Môđun của số phức \(z\cdot\overline{w}\) bằng
| \(5\sqrt{2}\) | |
| \(\sqrt{26}\) | |
| \(26\) | |
| \(50\) |
1 lời giải
Chọn phương án A.
Ta có \(\overline{w}=\sqrt{3^2+1^2}=\sqrt{10}\).
Suy ra \(z\cdot\overline{w}=\sqrt{10}+2\sqrt{10}i\).
Khi đó \(\left|z\cdot\overline{w}\right|=\sqrt{10+4\cdot10}=5\sqrt{2}\).