Ngân hàng bài tập
A
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\), \(AB=a\), \(BC=2a\), \(SA\) vuông góc với mặt phẳng đáy và \(SA=\sqrt{15}a\) (tham khảo hình vẽ).
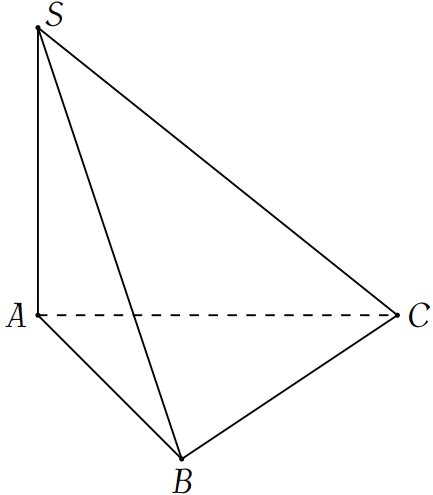
Góc giữa đường thẳng \(SC\) và mặt phẳng đáy bằng
| \(45^\circ\) | |
| \(30^\circ\) | |
| \(60^\circ\) | |
| \(90^\circ\) |
1 lời giải
Chọn phương án C.
Vì \(AC\) là hình chiếu vuông góc của \(SC\) lên mặt phẳng đáy. Do đó $$\left(SC,\left(ABC\right)\right)=\left(SC,AC\right)=\widehat{SCA}$$
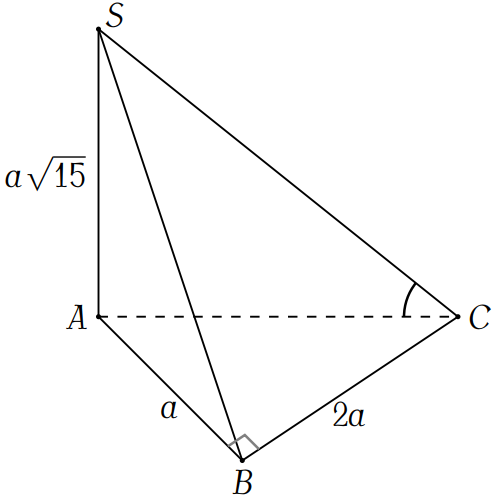
Trong tam giác \(ABC\) vuông tại \(B\) có $$AC=\sqrt{AB^2+BC^2}=\sqrt{a^2+4a^2}=a\sqrt{5}.$$
Trong tam giác $SAC$ vuông tại \(A\) có $$\tan\widehat{SCA}=\dfrac{SA}{AC}=\dfrac{a\sqrt{15}}{a\sqrt{5}}=\sqrt{3}\Rightarrow\widehat{SCA}=60^\circ.$$
Vậy \(\left(SC,\left(ABC\right)\right)=60^\circ\).
