Cho hình lăng trụ đứng \(ABC.A'B'C'\) có tất cả các cạnh bằng \(a\). Gọi \(M\) là trung điểm của \(CC'\) (tham khảo hình vẽ).
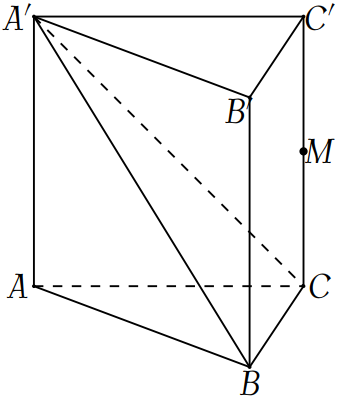
Khoảng cách từ \(M\) đến mặt phẳng \(\left(A'BC\right)\) bằng
| \(\dfrac{\sqrt{21}a}{14}\) | |
| \(\dfrac{\sqrt{2}a}{2}\) | |
| \(\dfrac{\sqrt{21}a}{7}\) | |
| \(\dfrac{\sqrt{2}a}{4}\) |
Chọn phương án A.
Gọi \(I\) là trung điểm của cạnh \(BC\), \(J\) là trung điểm cạnh \(B'C'\).
Đặt hình lăng trụ đã cho vào hệ trục tọa độ sao cho điểm \(I\) trùng với gốc tọa độ, điểm \(A\in Oy\), điểm \(J\in Oz\), điểm \(B,\,C\in Ox\).
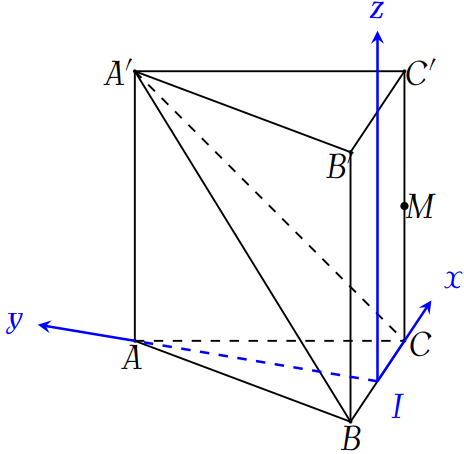
Ta có \(\overrightarrow{BC}=(1;0;0)\), \(\overrightarrow{BA'}=\left(\dfrac{1}{2};\dfrac{\sqrt{3}}{2};1\right)\).
Suy ra \(\left[\overrightarrow{BC},\overrightarrow{BA'}\right]=\left(0;-1;\dfrac{\sqrt{3}}{2}\right)\) là vectơ chỉ phương của \(\left(A'BC\right)\).
Do đó \(\left(A'BC\right)\colon-y+\dfrac{\sqrt{3}}{2}z=0\).
Vậy khoảng cách từ điểm \(M\) đến mặt phẳng \(\left(A'BC\right)\) bằng $$\mathrm{d}\left(M,\left(A'BC\right)\right)=\dfrac{\left|-0+\dfrac{\sqrt{3}}{2}\cdot\dfrac{1}{2}\right|}{\sqrt{(-1)^2+\left(\dfrac{\sqrt{3}}{2}\right)^2}}=\dfrac{\sqrt{21}}{14}$$
Do đó, \(\dfrac{\sqrt{21}a}{14}\) là kết quả cần tìm.
Chọn phương án A.
Ta có \(C'M\cap\left(A'BC\right)=C\), suy ra $$\dfrac{\mathrm{d}\left(M,\left(A'BC\right)\right)}{\mathrm{d}\left(C',\left(A'BC\right)\right)}=\dfrac{C'M}{C'C}=\dfrac{1}{2}$$
Ta có $$\begin{aligned}V_{C'.A'BC}&=\dfrac{1}{3}{V_{ABC.A'B'C'}}=\dfrac{1}{3}\cdot C'C\cdot S_{ABC}\\ &=\dfrac{1}{3}\cdot a\cdot\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^3\sqrt 3}{12}\end{aligned}$$
Lại có \(A'B=a\sqrt{2}\), \(CB=a\), \(A'C=a\sqrt{2}\).
Suy ra \(S_{A'BC}=\dfrac{a^2\sqrt{7}}{4}\).
Khi đó $$\begin{aligned}\mathrm{d}\left(C',\left(A'BC\right)\right)&=\dfrac{3V_{C'.A'BC}}{S_{A'BC}}=\dfrac{3\cdot\dfrac{a^3\sqrt{3}}{12}}{\dfrac{a^2\sqrt{7}}{4}}\\ &=\dfrac{a\sqrt{21}}{7}\end{aligned}$$
Vậy $$\begin{aligned}\mathrm{d}\left(M,\left(A'BC\right)\right)&=\dfrac{1}{2}\mathrm{d}\left(C',\left(A'BC\right)\right)\\ &=\dfrac{1}{2}\cdot\dfrac{a\sqrt{21}}{7}=\dfrac{a\sqrt{21}}{14}\end{aligned}$$
