Cho dãy số \(\left(u_n\right)\) xác định bởi \(\begin{cases}
u_1=2\\ u_{n+1}=\sqrt[3]{2+u_n^3},\,n\geq1
\end{cases}\). Số hạng tổng quát của \(\left(u_n\right)\) là
| \(u_n=\sqrt{6-2n}\) | |
| \(u_n=\sqrt[3]{6+2n}\) | |
| \(u_n=\sqrt[3]{5+3n}\) | |
| \(u_n=\sqrt{3n+1}\) |
Chọn phương án B.
Ta có $u_{n+1}=\sqrt[3]{2+u_n^3}\Leftrightarrow u_{n+1}^3=u_n^3+2$.
Đặt $v_n=u_n^3$. Khi đó $v_{n+1}=v_n+2$.
Vậy $\big(v_n\big)$ là một cấp số cộng với công sai $d=2$ và $v_1=u_1^3=2^3=8$.
Áp dụng công thức số hạng tổng quát của cấp số cộng ta được $$v_n=v_1+(n-1)d=8+2(n-1)=2n+6$$Vậy $u_n=\sqrt[3]{v_n}=\sqrt[3]{2n+6}$.
Chọn phương án B.
Bước 1. Tìm 5 số hạng đầu của dãy số truy hồi đã cho.

Bấm 2=
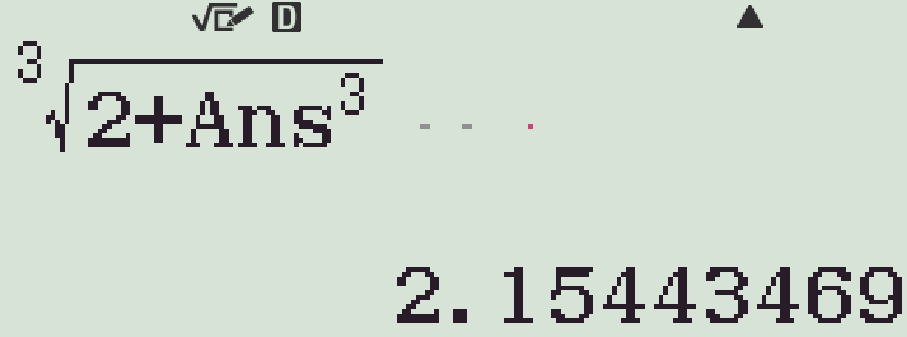
Bấm qsS2+MqD=
Mỗi lần bấm =, ta thu được một số hạng tiếp theo, kết quả là \(\sqrt[3]{8},\,\sqrt[3]{10},\,\sqrt[3]{12},\,\sqrt[3]{14},\,\sqrt[3]{16}\).
Bước 2. Dùng chức năng r liệt kê từng số hạng của từng phương án, ví dụ \(u_n=\sqrt[3]{6+2n}\).

Ta thu được kết quả là \(\sqrt[3]{8},\,\sqrt[3]{10},\,\sqrt[3]{12},\,\sqrt[3]{14},\,\sqrt[3]{16}\).
Chọn phương án B.
Ta có:
- \(u_1=2=\sqrt[3]{8}=\sqrt[3]{2\cdot1+6}\)
- \(u_2=\sqrt[3]{2+2^3}=\sqrt[3]{10}=\sqrt[3]{2\cdot2+6}\)
- \(u_3=\sqrt[3]{2+\left(\sqrt[3]{10}\right)^3}=\sqrt[3]{12}=\sqrt[3]{2\cdot3+6}\)
- \(u_4=\sqrt[3]{2+\left(\sqrt[3]{12}\right)^3}=\sqrt[3]{14}=\sqrt[3]{2\cdot4+6}\)
- \(u_5=\sqrt[3]{2+\left(\sqrt[3]{14}\right)^3}=\sqrt[3]{16}=\sqrt[3]{2\cdot5+6}\)
Theo đó, \(u_n=\sqrt[3]{6+2n}\), \(\forall n\in\Bbb{N}^*\).
