Ngân hàng bài tập
B
Cho hàm số \(y=f(x)\) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
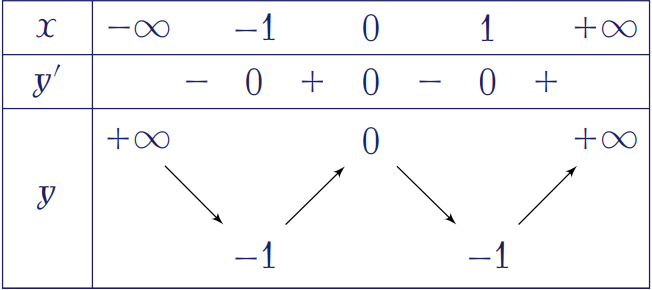
Tìm tất cả các giá trị thực của tham số \(m\) để phương trình \(f(x)-1=m\) có đúng \(2\) nghiệm.
| \(-2< m<-1\) | |
| \(m=-2\) hoặc \(m\geq-1\) | |
| \(m=-1\) hoặc \(m>0\) | |
| \(m=-2\) hoặc \(m>-1\) |
1 lời giải
Chọn phương án D.
Ta có \(f(x)-1=m\Leftrightarrow f(x)=m+1\).
Dựa vào bảng biến thiên ta thấy đường thẳng \(y=m+1\) cắt đồ thị \(y=f(x)\) tại \(2\) điểm khi $$\left[\begin{array}{l}m+1=-1\\ m+1>0\end{array}\right.\Leftrightarrow\left[\begin{array}{l}m=-2\\ m>-1\end{array}\right.$$
