Ngân hàng bài tập
A
Tìm \(m\) để đường thẳng \(y=2x+m\) cắt đồ thị hàm số \(y=\dfrac{2x}{x+1}\) tại \(2\) điểm phân biệt.
| \(m\in(-\infty;0)\cup(8;+\infty)\) | |
| \(m\in(-\infty;0]\cup[8;+\infty)\) | |
| \(m\in(0;8)\) | |
| \(m\in[0;8]\) |
1 lời giải
Chọn phương án A.
Phương trình hoành độ giao điểm: $$\dfrac{2x}{x+1}=2x+m\Leftrightarrow\dfrac{2x}{x+1}-2x=m$$
Đặt \(g(x)=\dfrac{2x}{x+1}-2x\) ta có $$g'(x)=\dfrac{2}{(x+1)^2}-2=\dfrac{-2x^2-4x}{(x+1)^2}$$
Cho \(g'(x)=0\Leftrightarrow-2x^2-4x=0\Leftrightarrow\left[\begin{array}{l}x=0\\ x=-2\end{array}\right.\)
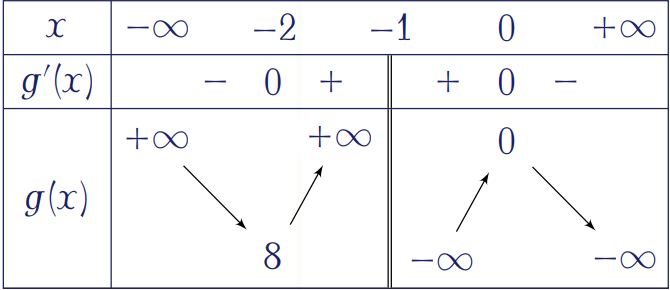
Theo đó, đường thẳng \(y=2x+m\) cắt đồ thị hàm số \(y=\dfrac{2x}{x+1}\) tại \(2\) điểm phân biệt khi \(m<0\) hoặc \(m>8\).
