Ngân hàng bài tập
A
Tìm \(m\) để đường thẳng \(y=x-m\) cắt đồ thị hàm số \(y=\dfrac{2x+1}{x+1}\) tại \(2\) điểm phân biệt.
| \(m<-1\) | |
| \(m>-5\) | |
| \(m<-5\) hoặc \(m>-1\) | |
| \(-5< m<-1\) |
1 lời giải
Chọn phương án C.
Phương trình hoành độ giao điểm: $$x-m=\dfrac{2x+1}{x+1}\Leftrightarrow x-\dfrac{2x+1}{x+1}=m$$
Đặt \(g(x)=x-\dfrac{2x+1}{x+1}\) ta có $$g'(x)=1-\dfrac{1}{(x+1)^2}=\dfrac{x^2+2x}{(x+1)^2}.$$
Cho \(g'(x)=0\Leftrightarrow x^2+2x=0\Leftrightarrow\left[\begin{array}{l}x=0\\ x=-2\end{array}\right.\)
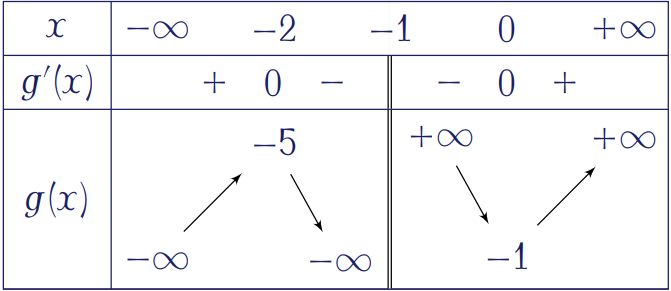
Theo đó, đường thẳng \(y=x-m\) cắt đồ thị hàm số \(y=\dfrac{2x+1}{x+1}\) tại \(2\) điểm phân biệt khi \(m<-5\) hoặc \(m>-1\).
Lại Trần Thế Vinh
18:46 14/09/2021
Có được bảng biến thiên rồi vậy làm sao để kết luận được như trên ạ !!!
Huỳnh Phú Sĩ
13:36 24/12/2022
Mình nên vẽ nháp đồ thị mô phỏng theo bảng biến thiên này, sau đó kẻ các đường thẳng $y=m$ song song với trục hoành để tìm trường hợp thỏa yêu cầu đề bài
