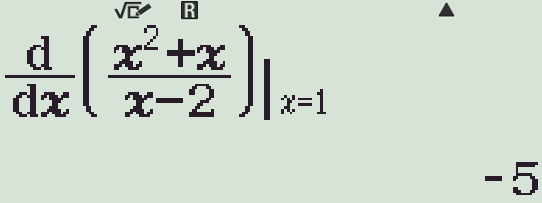Ngân hàng bài tập
C
Tính đạo hàm của hàm số \(f(x)=\dfrac{x^2+x}{x-2}\) tại điểm \(x=1\).
| \(f'(x)=-4\) | |
| \(f'(1)=-3\) | |
| \(f'(1)=-2\) | |
| \(f'(1)=-5\) |
1 lời giải
Chọn phương án D.
\(\begin{aligned}f'(x)&=\dfrac{\left(x^2+x\right)'(x-2)-\left(x^2+x\right)(x-2)'}{(x-2)^2}\\ &=\dfrac{(2x+1)(x-2)-\left(x^2+x\right)}{(x-2)^2}\\ &=\dfrac{x^2-4x-2}{(x-2)^2}.\end{aligned}\)
Khi đó \(f'(1)=\dfrac{1^2-4\cdot1-2}{(x-2)^2}=-5\).