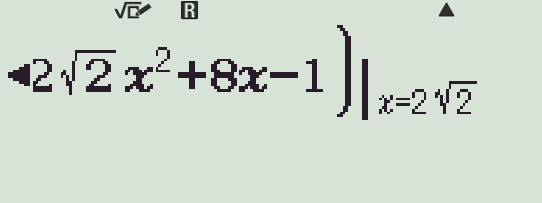Ngân hàng bài tập
B
Cho hàm số \(f(x)=\dfrac{x^3}{3}-2\sqrt{2}x^2+8x-1\) có đạo hàm \(f'(x)\). Tập hợp những giá trị của \(x\) để \(f'(x)=0\) là
| \(\left\{-2\sqrt{2}\right\}\) | |
| \(\left\{2;\sqrt{2}\right\}\) | |
| \(\left\{-4\sqrt{2}\right\}\) | |
| \(\left\{2\sqrt{2}\right\}\) |
1 lời giải
Chọn phương án D.
Ta có \(f'(x)=x^2-4\sqrt{2}x+8\).
Cho \(f'(x)=0\Leftrightarrow x^2-4\sqrt{2}x+8=0\Leftrightarrow x=2\sqrt{2}\).