Ngân hàng bài tập
A
Cho hàm số \(y=3x^3+x^2+1\) có đạo hàm \(y'\). Để \(y'\leq0\) thì \(x\) nhận các giá trị thuộc tập nào sau đây?
| \(\left[-\dfrac{2}{9};0\right]\) | |
| \(\left[-\dfrac{9}{2};0\right]\) | |
| \(\left(-\infty;-\dfrac{9}{2}\right]\cup\left[0;+\infty\right)\) | |
| \(\left(-\infty;-\dfrac{2}{9}\right]\cup\left[0;+\infty\right)\) |
1 lời giải
Chọn phương án A.
Ta có \(y'=9x^2+2x\).
Cho \(y'=0\Leftrightarrow\left[\begin{array}{l}
x=0\\ x=-\dfrac{2}{9}.
\end{array}\right.\)
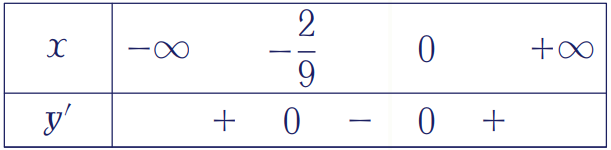
Suy ra \(y'\leq0\Leftrightarrow x\in\left[-\dfrac{2}{9};0\right]\).
