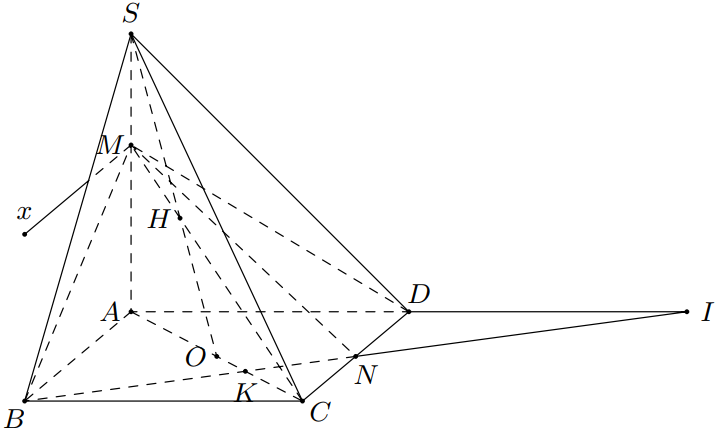
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành tâm $O$. Lấy điểm $M$ trên cạnh $SA$, trung điểm $CD$ là $N$. Tìm giao tuyến của các cặp mặt phẳng sau:
- $(SAC)$ và $(SBD)$.
- $(BMN)$ và $(SAD)$.
- $(BMN)$ và $(SAC)$.
- $(MCD)$ và $(SBD)$.
- $(MCD)$ và $(SAB)$.
a) $(SAC)$ và $(SBD)$ trong $(ABCD)$.
Ta có $S\in(SAC)\cap(SBD)$ (1)
Gọi $O=AC\cap BD$ suy ra $O\in(SAC)\cap(SBD)$ (2)
Từ (1), (2) suy ra $(SAC)\cap(SBD)=SO$.
b) $(BMN)$ và $(SAD)$.
Gọi $I=BN\cap AD$ trong $(ABCD)$.
Suy ra $I\in(BMN)\cap(SAD)$ (1)
Mặt khác $M\in(SAD)\cap(BMN)$ (2)
Từ (1) và (2) suy ra $(BMN)\cap(SAD)=MI$.
c) $(BMN)$ và $(SAC)$.
Gọi $K=AC\cap BN$ trong $(ABCD)$.
Suy ra $K\in(BMN)\cap(SAC)$ (1)
Mặt khác $M\in(BMN)\cap(SAC)$ (2)
Từ (1) và (2) suy ra $MK=(BMN)\cap(SAC)$.
d) $(MCD)$ và $(SBD)$.
Ta có $D\in(MCD)\cap(SBD)$ (1)
Gọi $H=MC\cap SO$ trong $(SAC)$.
Suy ra $H\in(SAC)\cap(MCD)$ (2)
Từ (1) và (2) suy ra $HM=(MCD)\cap (SAC)$.
e) $(MCD)$ và $(SAB)$.
Ta có $M\in(MCD)\cap(SAB)$ (1)
Mặt khác $\begin{cases}AB\parallel CD\\ AB\in(SAB)\\ CD\in(MCD).\end{cases}$ (2)
Từ (1) và (2) suy ra $Mx=(SAB)\cap(MCD)$ với $Mx\parallel AB$.
