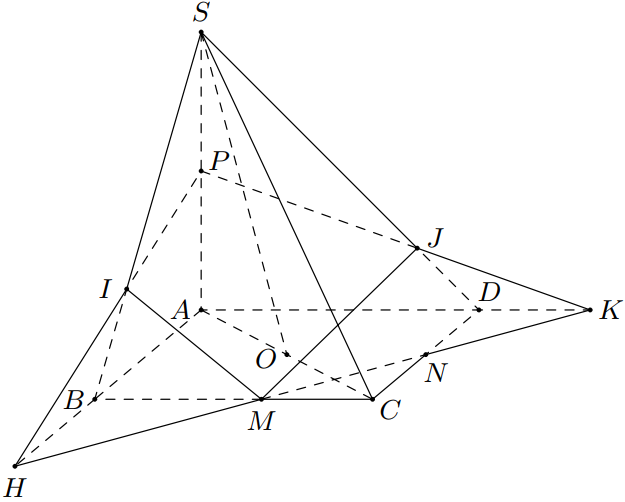
a) $(SAC)$ và $(SBD)$.
Ta có $S\in(SAC)\cap(SBD)$ (1)
Gọi $O=AC\cap BD$ trong $(ABCD)$, suy ra $O\in(SAC)\cap(SBD)$ (2)
Từ (1) và (2) suy ra $SO=(SAC)\cap(SBD)$.

b) $(MNP)$ và $(SAB)$.
Trong $(ABCD)$, gọi $H=MN\cap AB$, suy ra $H\in(MNP)\cap (SAB)$. (1)
Mặt khác $P\in(MNP)\cap(SAB)$ (2)
Từ (1) và (2) suy ra $PH=(MNP)\cap(SAB)$.

c) $(MNP)$ và $(SAD)$.
Ta có $P\in(SAD)\cap(MNP)$ (1)
Gọi $K=MN\cap AD$ trong $(ABCD)$, khi đó $K\in(MNP)\cap(SAD)$ (2)
Từ (1) và (2) suy ra $PK=(MNP)\cap(SAD)$.

d) $(MNP)$ và $(SBC)$.
Trong $(SBC)$, gọi $I=PH\cap SB$, khi đó $I\in(MNP)\cap(SBC)$ (1)
Mặt khác $M\in(MNP)\cap(SBC)$ (2)
Từ (1) và (2) suy ra $MI=(MNP)\cap(SBC)$.

e) $(MNP)$ và $(SCD)$.
Trong $(SCD)$, gọi $J=PK\cap SD$, khi đó $J\in(MNP)\cap(SCD)$ (1)
Mặt khác $N\in(MNP)\cap(SCD)$ (2)
Từ (1) và (2) suy ra $NJ=(MNP)\cap(SCD)$.