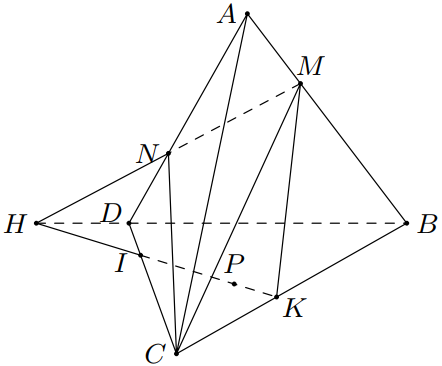
a) $(CMN)$ và $(BCD)$.
Ta có $C\in(CMN)\cap(BCD)$ (1)
Trong $(ABD)$, gọi $H=MN\cap DB$, khi đó $H\in(CMN)\cap(BCD)$ (2)
Từ (1) và (2) suy ra $CH=(CMN)\cap(BCD)$.

b) $(MNP)$ và $(CAD)$.
Ta có $N\in(MNP)\cap(CDA)$ (1)
Trong $(BCD)$, gọi $I=HO\cap CD$, khi đó $I\in(MNP)\cap(ACD)$ (2)
Từ (1) và (2) suy ra $NI=(MNP)\cap(ACD)$.

c) $(MNP)$ và $(ABC)$.
Ta có $M\in(MNP)\cap(ABC)$ (1)
Trong $(BCD)$, gọi $K=HP\cap BC$, khi đó $K\in(MNP)\cap(ABC)$ (2)
Từ (1) và (2) suy ra $KM=(MNP)\cap(ABC)$.