Ngân hàng bài tập
A
Cho hình chóp $S.ABC$ có $SA=SB=SC$ và đáy là tam giác $ABC$ vuông cân tại $A$. Trong các mệnh đề dưới đây, có bao nhiêu mệnh đề đúng?
- (E) $S.ABC$ là hình chóp đều.
- (F) $\triangle ABC$ có tâm đường tròn ngoại tiếp là trung điểm $BC$.
- (G) Chân đường cao của hình chóp trùng với tâm đường tròn ngoại tiếp $\triangle ABC$.
| $0$ | |
| $1$ | |
| $2$ | |
| $3$ |
1 lời giải
Chọn phương án C.
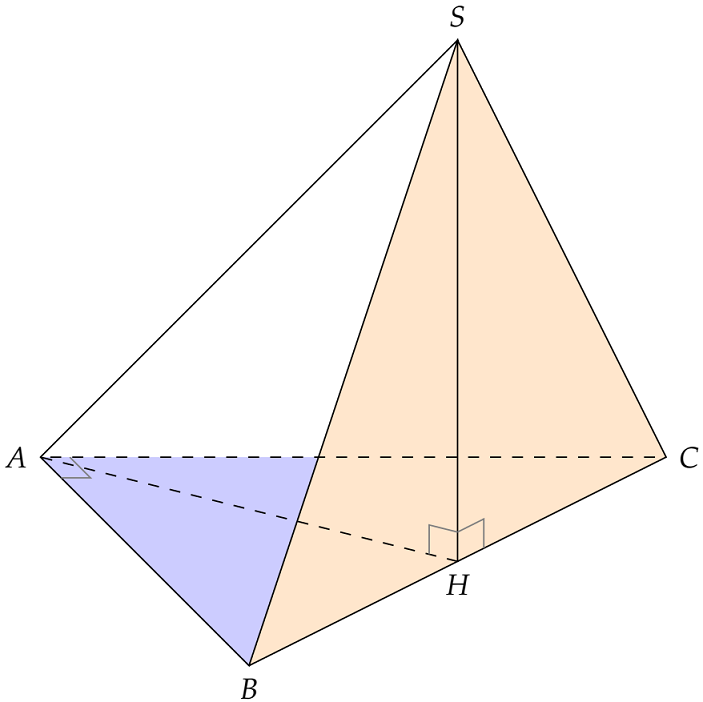
- Vì $ABC$ không phải tam giác đều nên (E) sai.
- Vì $ABC$ vuông cân tại $A$ nên (F) đúng.
- Gọi $SH$ là đường cao của hình chóp $S.ABC$. Khi đó, vì ba tam giác $SHA$, $SHB$, $SHC$ đều vuông tại $H$, có chung cạnh $SH$ và $SA=SB=SC$ nên chúng bằng nhau (cạnh - góc - cạnh). Do đó, $HA=HB=HC$. Nói cách khác, $H$ là tâm đường tròn ngoại tiếp $\triangle ABC$. Suy ra (G) đúng.
