Ngân hàng bài tập
S
Tìm tập xác định $\mathscr{D}$ của hàm số $$y=\sqrt{\sqrt{x^2+2x+2}-x-1}$$
| $\mathscr{D}=\Bbb{R}\setminus\left\{-1\right\}$ | |
| $\mathscr{D}=\Bbb{R}$ | |
| $\mathscr{D}=\left(-\infty;-1\right)$ | |
| $\mathscr{D}=\left[-1;+\infty\right)$ |
2 lời giải
Chọn phương án B.
Dùng chức năng r của máy tính cầm tay.
Bước 1. Kiểm tra với $x=-1$.

Kết quả bằng $1$, tức là hàm số xác định với $x=-1$, do đó loại phương án A và C.
Bước 2. Kiểm tra với $x\notin[-1;+\infty)$, ví dụ $x=-2$.
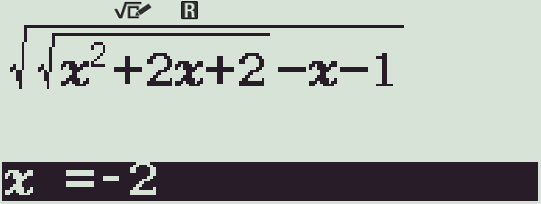
Kết quả xấp xỉ $1,55$, tức là xác định. Vậy loại phương án D.
Chọn phương án B.
Điều kiện: $\sqrt{x^2+2x+2}-x-1\geq0\Leftrightarrow\sqrt{x^2+2x+2}\geq x+1$ (1)
Vì $x^2+2x+2>(x+1)^2\geq0$, $\forall x\in\mathbb{R}$ nên (1) đúng với $\forall x\in\mathbb{R}$.
Vậy hàm số đã cho có tập xác định $\mathscr{D}=\Bbb{R}$.
