Ngân hàng bài tập
A
Tìm các giá trị của $m$ để phương trình $-2x^2-4x+3=m$ có nghiệm.
| $1\leq m\leq5$ | |
| $-4\leq m\leq0$ | |
| $0\leq m\leq4$ | |
| $m\leq 5$ |
2 lời giải
Chọn phương án D.
Đồ thị của hàm số $y=-2x^2-4x+3$ là parabol úp xuống, có điểm cao nhất là đỉnh $I\left(-1;5\right)$.
Đồ thị của hàm số $y=m$ là đường thẳng song song với trục hoành.
Để phương trình $-2x^2-4x+3=m$ có nghiệm thì đường thẳng $y=m$ cắt parabol $y=-2x^2-4x+3$ ít nhất một điểm, tức là $m\leq5$.
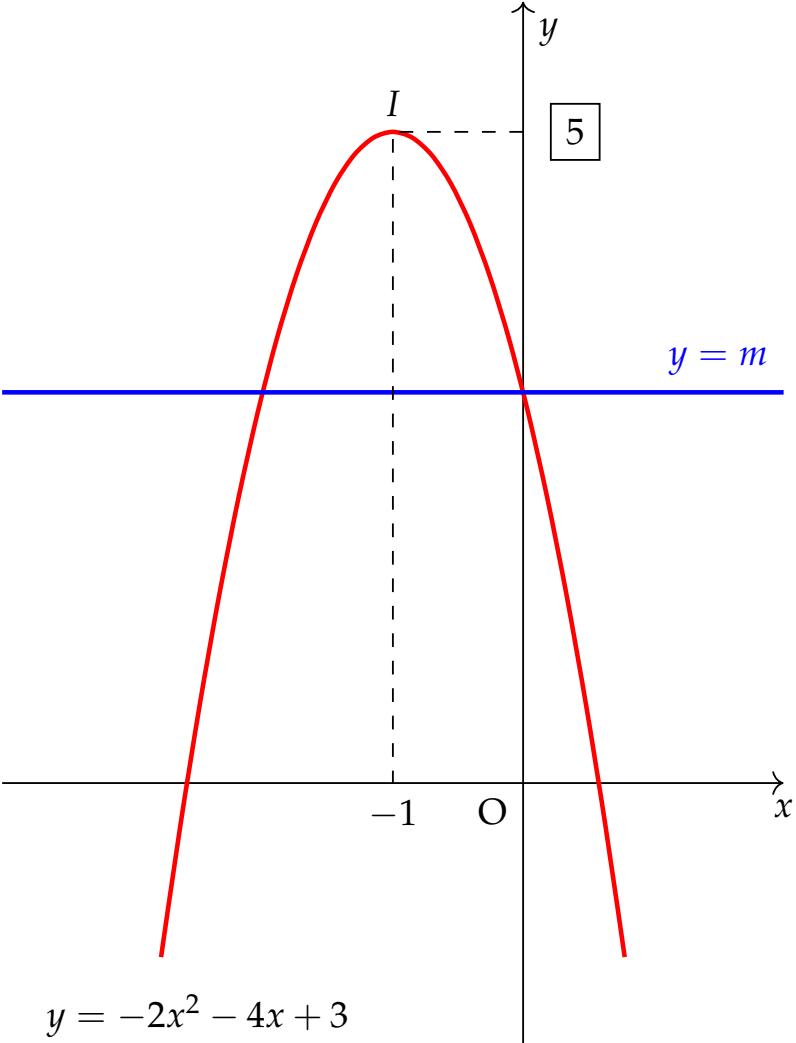
Cách này được sử dụng phổ biến trong các bài toán tương giao đồ thị của Giải Tích 12
Chọn phương án D.
Phương trình $-2x^2-4x+3=m$ có nghiệm khi và chỉ khi phương trình $-2x^2-4x+3-m=0$ có nghiệm.
$$\begin{aligned}
\Leftrightarrow&\Delta'\geq0\\
\Leftrightarrow&\left(-2\right)^2-\left(-2\right)\left(3-m\right)\geq0\\
\Leftrightarrow&10-2m\geq0\\
\Leftrightarrow&m\leq5.
\end{aligned}$$
