Ngân hàng bài tập
B
Cho biểu thức $f\left(x\right)=\left(x+5\right)\left(3-x\right)$. Tìm tập hợp các giá trị $x$ để $f\left(x\right)\leq0$.
| $\left(-\infty;-5\right)\cup\left(3;+\infty\right)$ | |
| $\left(3;+\infty\right)$ | |
| $\left(-5;-3\right)$ | |
| $\left(-\infty;-5\right]\cup\left[3;+\infty\right)$ |
1 lời giải
Chọn phương án D.
Xét dấu $f\left(x\right)$:
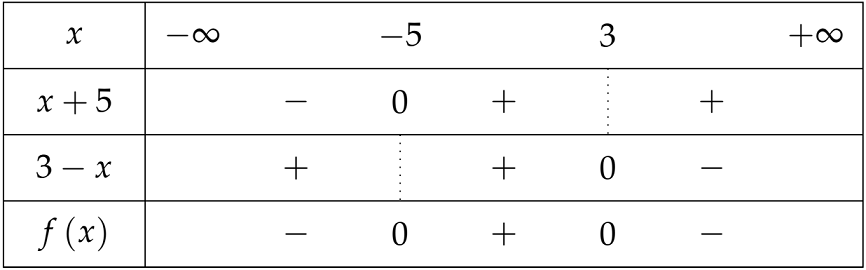
Theo đó, để $f\left(x\right)\leq0$ thì $x\in\left(-\infty;-5\right]\cup\left[3;+\infty\right)$.
