Ngân hàng bài tập
A
Hàm số $y=\left(3-x\right)\left(x+2\right)^2\left(x-2\right)^3$ nhận giá trị dương trên khoảng nào dưới đây?
| $\left(-2;2\right)$ | |
| $\left(3;+\infty\right)$ | |
| $\left(2;3\right)$ | |
| $\left(-\infty;-2\right)$ |
1 lời giải
Chọn phương án C.
Bảng xét dấu: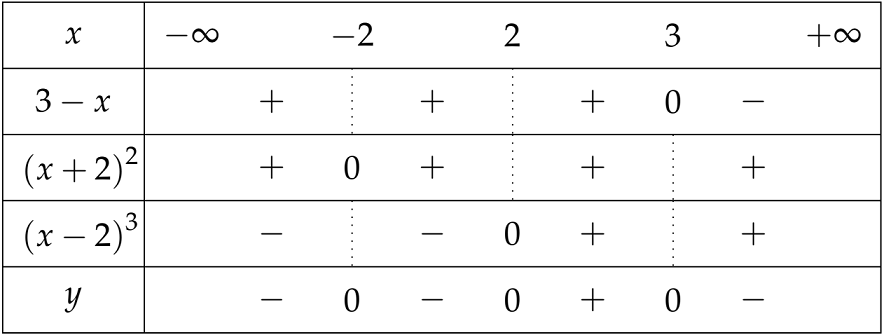
Theo đó, $y>0\Leftrightarrow x\in\left(2;3\right)$.
Lưu ý:
- $\left(x+2\right)^2\geq0,\,\forall x\in\Bbb{R}$ nên thực tế không cần xét dấu.
- $\left(x-2\right)^3=\left(x-2\right)\cdot\left(x-2\right)^2$, cùng dấu với $x-2$. Do đó, để xét dấu $\left(x-2\right)^3$ ta chỉ cần xét dấu $x-2$.
