Ngân hàng bài tập
A
Tìm tập xác định của hàm số $y=\sqrt{\dfrac{x^2+4x+5}{2x^2+3x+1}}$.
| $\left(-\infty;-1\right]\cup\left[-\dfrac{1}{2};+\infty\right)$ | |
| $\left[-1;-\dfrac{1}{2}\right]$ | |
| $\left(-\infty;-1\right)\cup\left(-\dfrac{1}{2};+\infty\right)$ | |
| $\left(-1;-\dfrac{1}{2}\right)$ |
1 lời giải
Chọn phương án C.
Điều kiện xác định: $\dfrac{x^2+4x+5}{2x^2+3x+1}\geq0$.
Bảng xét dấu: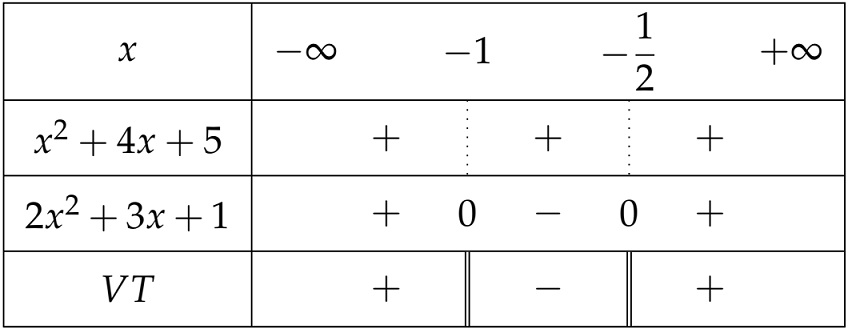
Theo đó, tập xác định $D=\left(-\infty;-1\right)\cup\left(-\dfrac{1}{2};+\infty\right)$.
