Ngân hàng bài tập
A
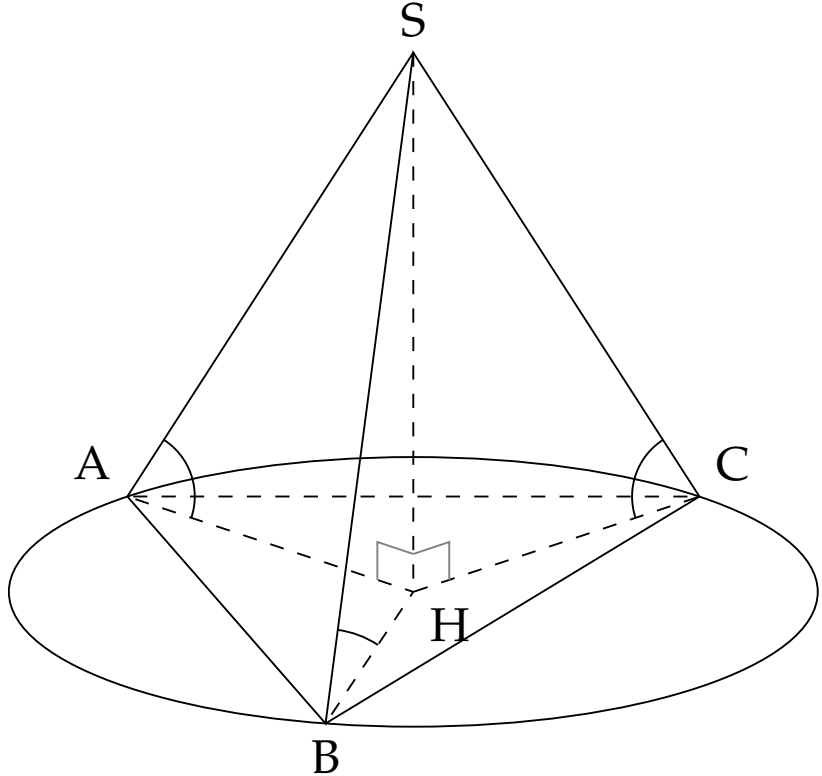
Cho hình chóp $S.ABC$ có góc tạo bởi các cạnh bên và mặt đáy bằng nhau. Gọi $H$ là hình chiếu vuông góc của $S$ trên mặt đáy. Phát biểu nào sau đây đúng nhất?
| $S.ABC$ là hình chóp đều | |
| $H$ là trực tâm của $\triangle ABC$ | |
| $H$ là tâm đường tròn ngoại tiếp $\triangle ABC$ | |
| $H$ là tâm đường tròn nội tiếp $\triangle ABC$ |
1 lời giải
Chọn phương án C.
$\begin{cases}
\left(SA,\left(ABC\right)\right)=\widehat{SAH}\\ \left(SB,\left(ABC\right)\right)=\widehat{SBH}\\
\left(SC,\left(ABC\right)\right)=\widehat{SCH}
\end{cases}\Rightarrow\widehat{SAH}=\widehat{SBH}=\widehat{SCH}$.
Do đó, ba tam giác vuông $SAH$, $SBH$, $SCH$ đôi một bằng nhau.
$\Rightarrow HA=HB=HC$.
$\Rightarrow$ $H$ là tâm đường tròn ngoại tiếp $\triangle ABC$.
