Ngân hàng bài tập
A
Cho hình chóp đều $S.ABCD$ có đáy bằng $2$, cạnh bên bằng $3$. Gọi $\varphi$ là góc giữa cạnh bên và mặt đáy. Mệnh đề nào sau đây đúng?
| $\tan\varphi=\sqrt{7}$ | |
| $\varphi=60^\circ$ | |
| $\varphi=45^\circ$ | |
| $\tan\varphi=\dfrac{\sqrt{14}}{2}$ |
1 lời giải
Chọn phương án D.
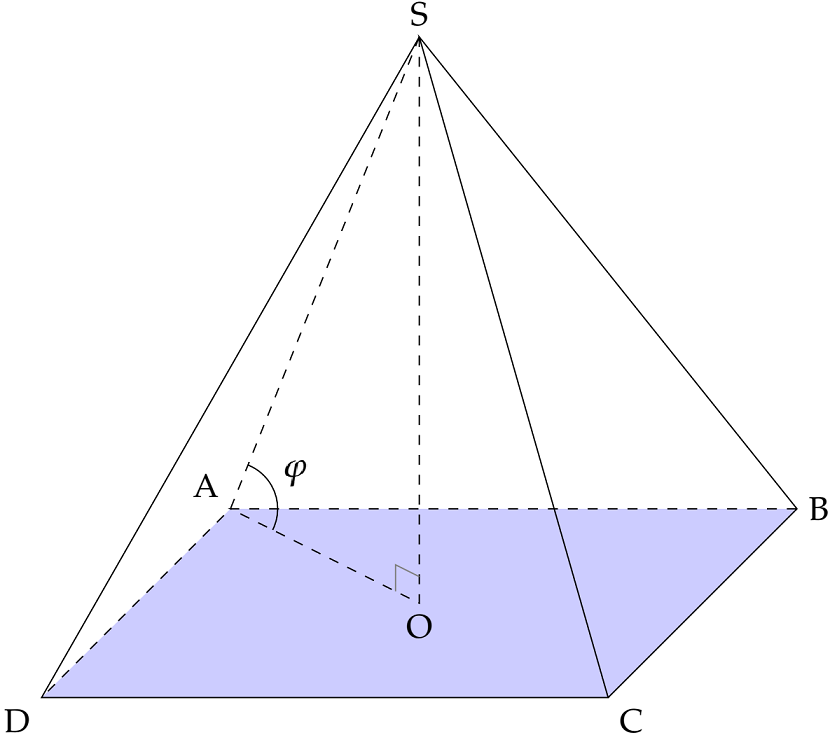
$OA$ là hình chiếu vuông góc của $SA$ trên mặt $\left(ABCD\right)$.
$\Rightarrow\left(SA,\left(ABCD\right)\right)=\left(SA,OA\right)=\widehat{SAO}=\varphi$.
$\triangle SAO$ vuông tại $O$, có $\begin{cases}SA=3\\ AO=\dfrac{AC}{2}=\dfrac{2\sqrt{2}}{2}=\sqrt{2}\end{cases}$
$\Rightarrow\cos\varphi=\dfrac{AO}{SA}=\dfrac{\sqrt{2}}{3}$.
$\Rightarrow\tan^2\varphi=\dfrac{1}{\cos^2\varphi}-1=\dfrac{7}{2}$.
$\Rightarrow\tan\varphi=\dfrac{\sqrt{14}}{2}$.
