Cho hình chóp $S.ABC$ có góc tạo bởi các mặt bên và mặt đáy bằng nhau. Gọi $H$ là hình chiếu vuông góc của $S$ trên mặt đáy. Phát biểu nào sau đây đúng nhất?
| $S.ABC$ là hình chóp đều | |
| $H$ là trực tâm của $\triangle ABC$ | |
| $H$ là tâm đường tròn ngoại tiếp $\triangle ABC$ | |
| $H$ là tâm đường tròn nội tiếp $\triangle ABC$ |
Chọn phương án D.
Gọi $M$, $N$, $K$ lần lượt là hình chiếu vuông góc của $H$ trên các cạnh $BC$, $CA$, $AB$.
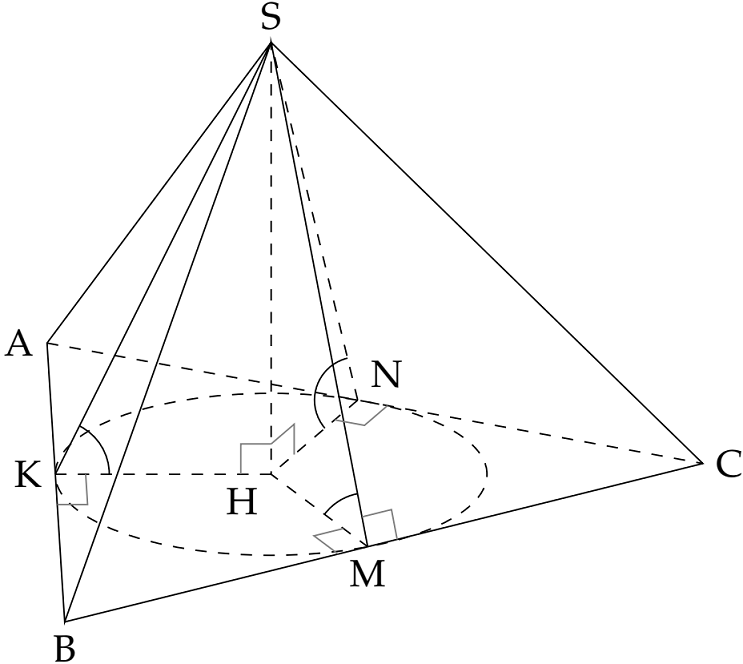
Ta có $\begin{cases}
BC=\left(SBC\right)\cap\left(ABC\right)\\
BC\bot HM\\
BC\bot SM\,\,\left(BC\bot SH\text{ và }BC\bot HM\right)
\end{cases}$
$\Rightarrow\left(\left(SBC\right),\left(ABC\right)\right)=\widehat{SMH}$.
Tương tự, ta cũng có $$\begin{cases}
\left(\left(SCA\right),\left(ABC\right)\right)=\widehat{SNH}\\
\left(\left(SAB\right),\left(ABC\right)\right)=\widehat{SKH}
\end{cases}$$
Theo đề, ta có
$\widehat{SMH}=\widehat{SNH}=\widehat{SKH}$.
Do đó, ba tam giác vuông $SMH$, $SNH$, $SKH$ đôi một bằng nhau.
$\Rightarrow HM=HN=HK$.
$\Rightarrow$ $H$ là tâm đường tròn nội tiếp $\triangle ABC$.
