Ngân hàng bài tập
A
Cho hình chóp $S.ABC$ có cạnh bên $SA=a\sqrt{3}$ và hợp với đáy một góc $60^\circ$. Tính khoảng cách từ điểm $S$ đến mặt đáy.
| $a\sqrt{3}$ | |
| $\dfrac{3a}{2}$ | |
| $\dfrac{a\sqrt{3}}{2}$ | |
| $2a$ |
1 lời giải
Chọn phương án B.
Gọi $H$ là hình chiếu vuông góc của $S$ trên mặt đáy $\Rightarrow d\left(S,\left(ABC\right)\right)=SH$.
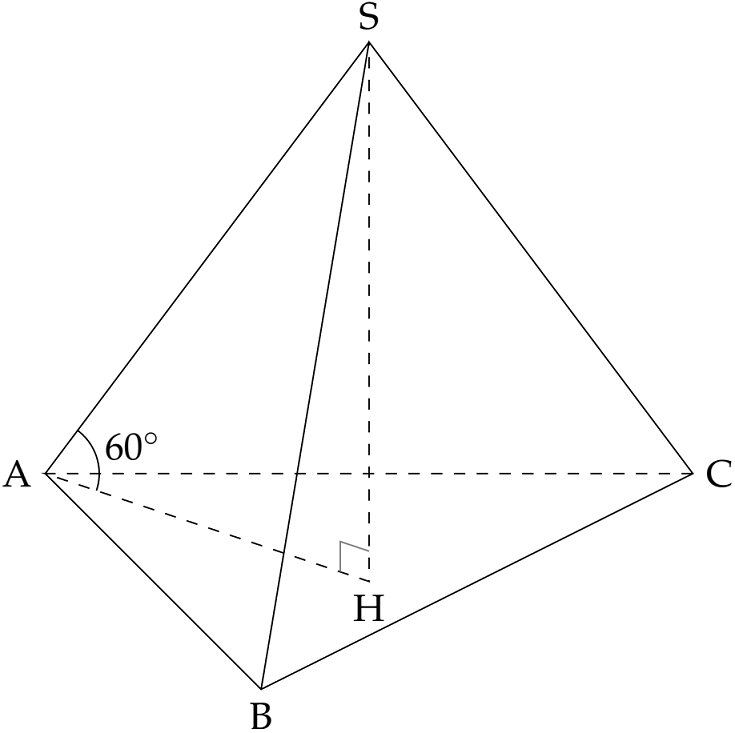
Theo đề, $\left(SA,\left(ABC\right)\right)=\widehat{SAH}=60^\circ$.
Vì $\triangle SHA$ vuông tại $H$ nên $\sin\widehat{SAH}=\dfrac{SH}{SA}$.
$\Rightarrow SH=SA\cdot\sin\widehat{SAH}=a\sqrt{3}\cdot\sin60^\circ=\dfrac{3a}{2}$.
