Ngân hàng bài tập
A
Cho tứ diện $OABC$ có $OA$, $OB$, $OC$ đôi một vuông góc. Gọi $OH$ là đường cao của tứ diện. Khi đó $H$ là
| Trọng tâm $\triangle ABC$ | |
| Trực tâm $\triangle ABC$ | |
| Tâm đường tròn nội tiếp $\triangle ABC$ | |
| Tâm đường tròn ngoại tiếp $\triangle ABC$ |
1 lời giải
Chọn phương án B.
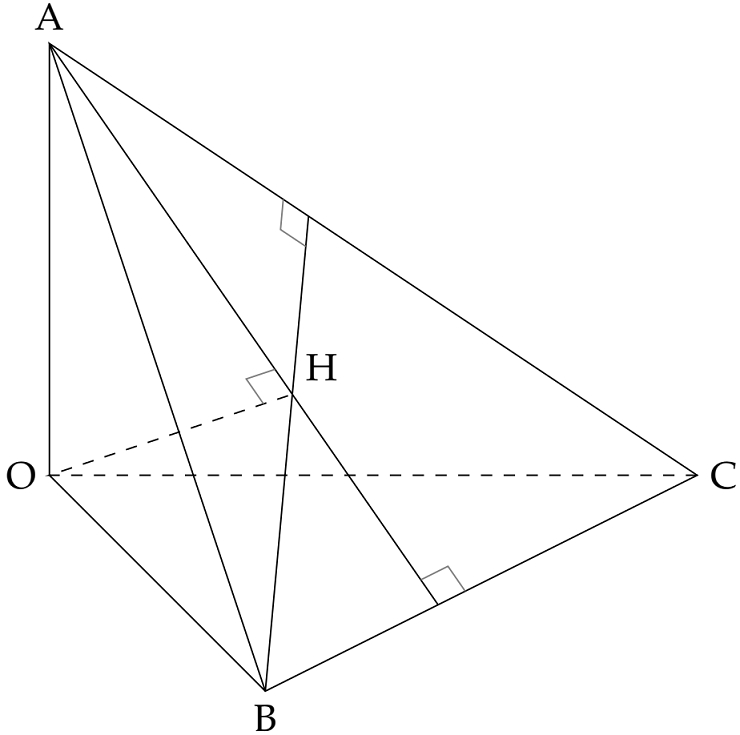
Vì $\begin{cases}OH\bot\left(ABC\right)\\ OA\bot\left(OBC\right)\end{cases}$ nên $\begin{cases}BC\bot OH\\ BC\bot OA\end{cases}\Rightarrow BC\bot AH$.
Tương tự, ta cũng có $\begin{cases}AC\bot BH\\ AB\bot CH\end{cases}$.
Suy ra $H$ là trực tâm của $\triangle ABC$.
