Cho hình lăng trụ $ABC.DEF$ có $BCD$ là tam giác đều cạnh $a\sqrt{3}$ và mặt phẳng $\left(BCD\right)$ hợp với đáy một góc $60^\circ$. Biết tam giác $ABC$ cân tại $A$, tính chiều cao của hình lăng trụ.
| $\dfrac{a\sqrt{3}}{2}$ | |
| $\dfrac{3a\sqrt{3}}{2}$ | |
| $\dfrac{3a\sqrt{3}}{4}$ | |
| $\dfrac{3a}{4}$ |
Chọn phương án C.
Gọi $M$ là trung điểm $BC$.
Vì $\triangle ABC$ cân tại $A$ và $\triangle DBC$ đều nên $\begin{cases}BC\bot AM\\ BC\bot DM\end{cases}$ (1).
Mà $BC=\left(ABC\right)\cap\left(DBC\right)$.
Do đó, $\left(\left(ABC\right),\left(DBC\right)\right)=\left(AM,DM\right)=\widehat{AMD}=60^\circ$.
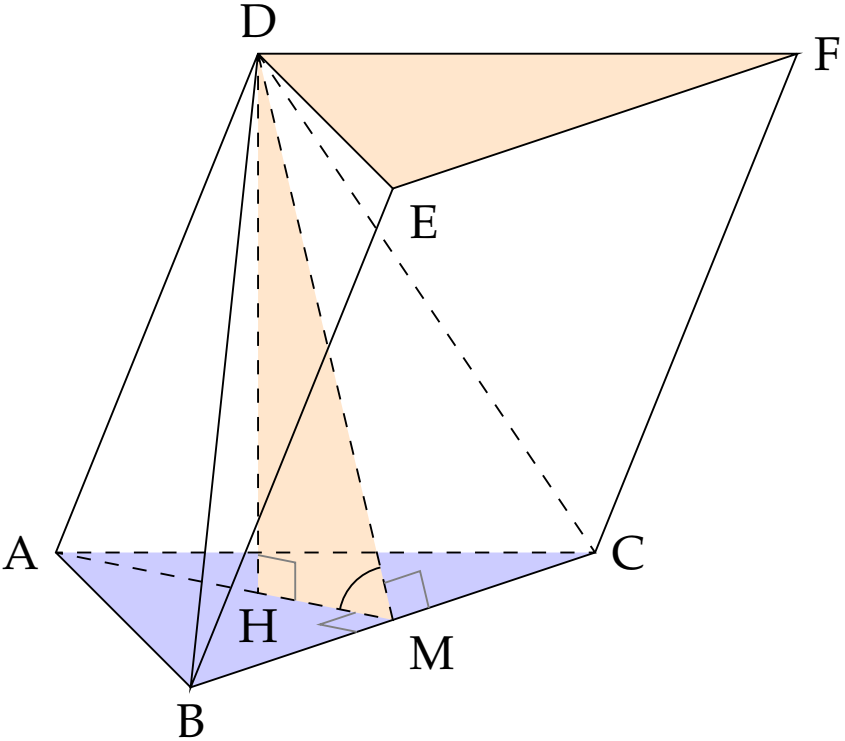
Trong $\left(AMD\right)$, dựng $DH\bot AM$ (2).
Từ (1) ta có $BC\bot\left(AMD\right)\Rightarrow DH\bot BC$ (3).
Từ (2) và (3) suy ra $DH\bot\left(ABC\right)$.
$\Rightarrow$ DH là đường cao của hình lăng trụ.
Xét $\triangle MHD$ có $\begin{cases}\widehat{M}=60^\circ\\ DM=a\sqrt{3}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{3a}{2}\end{cases}$
Khi đó $\sin\widehat{M}=\dfrac{DH}{DM}$.
$\Rightarrow DH=DM\cdot\sin\widehat{M}=\dfrac{3a}{2}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{3a\sqrt{3}}{4}$.
