Ngân hàng bài tập
B
Cho hình lập phương $ABCD.EFGH$ có cạnh bằng $a$. Tính độ dài đường chéo của hình lập phương.
| $3a$ | |
| $a\sqrt{2}$ | |
| $a\sqrt{3}$ | |
| $\dfrac{a\sqrt{3}}{2}$ |
1 lời giải
Chọn phương án C.
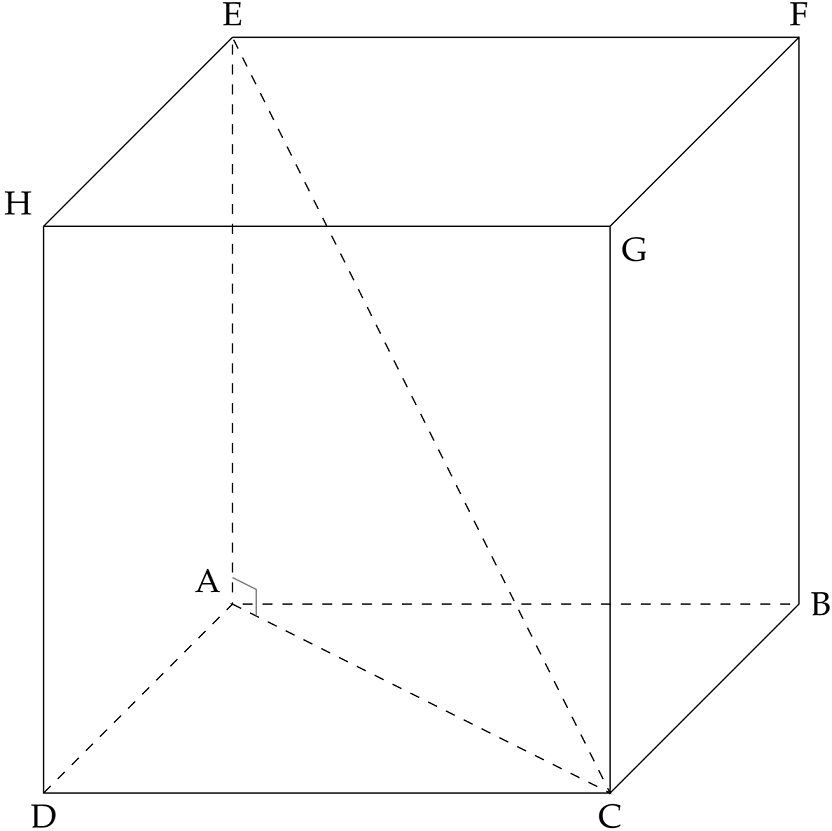
$EC$ là một trong các đường chéo của hình lập phương $ABCD.EFGH$.
$\triangle EAC$ vuông tại $A$ và $\begin{cases}AE=a\\ AC=a\sqrt{2}\end{cases}$.
$\Rightarrow EC^2=AE^2+AC^2=3a^2$.
$\Rightarrow EC=a\sqrt{3}$.
