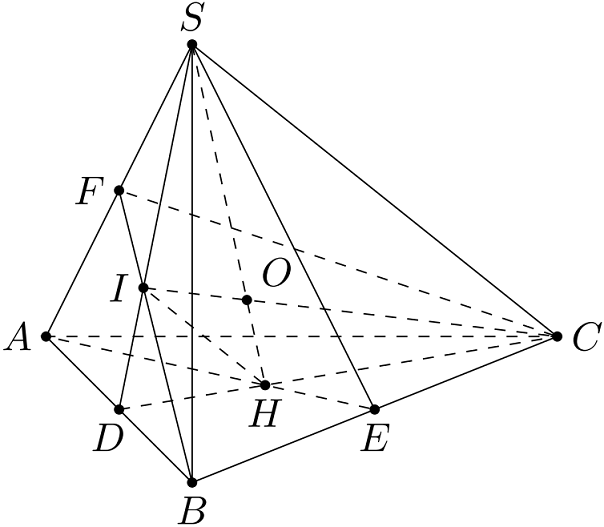
a) Trong $(ABC)$, gọi $H=AE\cap CD$.
Ta có $\begin{cases}H\in CD,\,CD\subset(SCD)\Rightarrow H\in(SCD)\\ H\in AE,\,AE\subset(SAE)\Rightarrow H\in(SAE)\end{cases}$
Suy ra $H\in(SCD)\cap(SAE)$.

Lại có $S\in(SCD)\cap(SAE)$. Suy ra $(SCD)\cap(SAE)=SH$.

b) Trong $(SAB)$, gọi $I=BF\cap SD$.
Ta có $\begin{cases}I\in SD,\,SD\subset(SCD)\Rightarrow I\in(SCD)\\ I\in BF,\,BF\subset(BFC)\Rightarrow I\in(BFC)\end{cases}$
Suy ra $I\in(SCD)\cap(BFC)$.

Lại có $C\in(SCD)\cap(BFC)$. Suy ra $(SCD)\cap(BFC)=CI$.

c) Trong $(SCD)$, gọi $O=SH\cap CI$.
Ta có $SD$, $BF$ là hai đường trung tuyến của $\triangle SAB \Rightarrow I$ là trọng tâm của $\triangle SAB\Rightarrow \dfrac{ID}{SD}=\dfrac{1}{3}.$

Tương tự, ta có $H$ là trọng tâm của $\triangle ABC\Rightarrow \dfrac{HD}{CD}=\dfrac{1}{3}$.

Do đó $\dfrac{ID}{SD}=\dfrac{HD}{CD}=\dfrac{1}{3}\Rightarrow IH\parallel SC$
Suy ra $\dfrac{IH}{SC}=\dfrac{ID}{SD}=\dfrac{1}{3}$ (hệ quả định lý Thales).

Mặt khác, vì $IH\parallel SC$ nên $\dfrac{IH}{SC}=\dfrac{OI}{OC}=\dfrac{OH}{OS}$.
Do đó $\dfrac{OH}{OS}=\dfrac{1}{3}$.