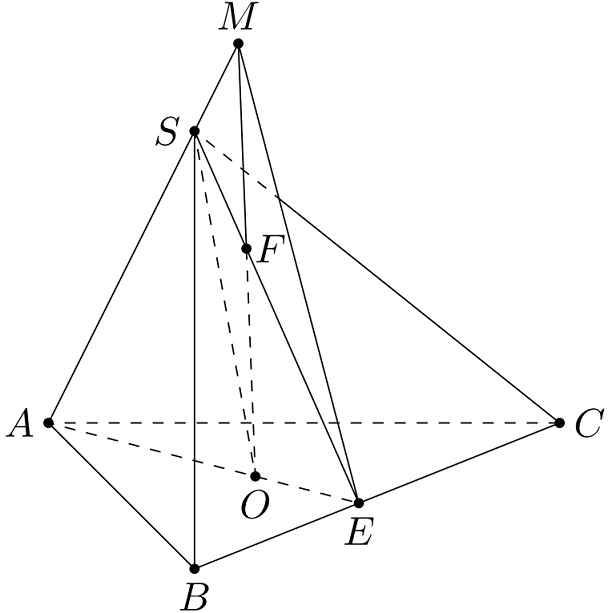
a) Trong $(ABC)$, gọi $E=OA\cap BC$.
Ta có: $\begin{cases}E\in OA,\,OA\subset(SOA)\Rightarrow E\in(SOA)\\
E\in BC\end{cases}$
Suy ra $E=BC\cap(SOA)$.

b) Chọn mặt phẳng phụ $(MAE)$ chứa $MO$.

Xét hai mặt phẳng $(MAE)$ và $(SBC)$.
Ta có: $\begin{cases}S\in AM,\,AM\subset(MAE)\Rightarrow S\in(MAE)\\
S\in(SBC)\end{cases}$
Suy ra $S\in(MAE)\cap(SBC)$ (1)

Mặt khác: $\begin{cases}E\in AO,\,BC\subset(MAE)\Rightarrow E\in(MAE)\\ E\in BC,\,BC\subset(SBC)\end{cases}$
Suy ra $E\in(SBC)\Rightarrow E\in(MAE)\cap(SBC)$ (2)

Từ (1) và (2)$\Rightarrow(MAE)\cap(SBC)=SE$.

Trong $(MAE)$, gọi $F=MO\cap SE$.
Khi đó $\begin{cases}F\in MO\\ F\in SE,\,SE\subset(SBC)\end{cases}$
Suy ra $F=MO\cap(SBC)$.