Ngân hàng bài tập
Cho tứ diện $SABC$ có hai điểm $M$, $N$ lần lượt thuộc hai cạnh $SA$, $SB$ và $O$ là điểm nằm trong tam giác $ABC$. Hãy tìm
- Giao điểm của đường thẳng $AB$ và $(SOC)$.
- Giao điểm của đường thẳng $MN$ và $(SOC)$.
- Giao điểm của đường thẳng $SO$ và $(CMN)$.
1 lời giải
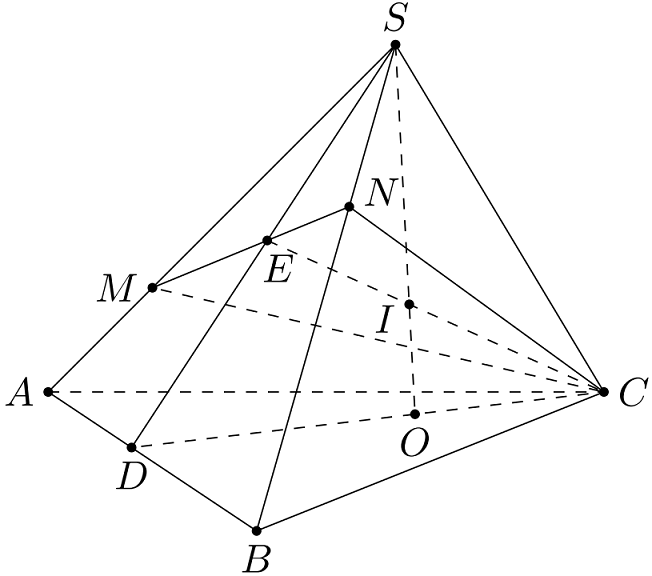
a) Trong $(ABC)$, gọi $D=CO\cap AB$.
Ta có $\begin{cases}D\in OC,\,OC\subset(SOC)\Rightarrow D\in(SOC)\\ D\in AB\end{cases}$
Suy ra $AB\cap(SOC)=D$.
b) Trong $(SAB)$, gọi $E=MN\cap SD$.
Ta có $\begin{cases}E\in SD,\,SD\subset(SOC)\Rightarrow E\in(SOC)\\ E\in MN\end{cases}$
Suy ra $E=MN\cap(SOC)$.
c) Trong $(SCD)$, gọi $I=EC\cap SO$.
Ta có $\begin{cases}I\in EC,\,EC\subset(CMN)\Rightarrow I\in(CMN)\\ I\in SO\end{cases}$
Suy ra $I=SO\cap(CMN)$.
