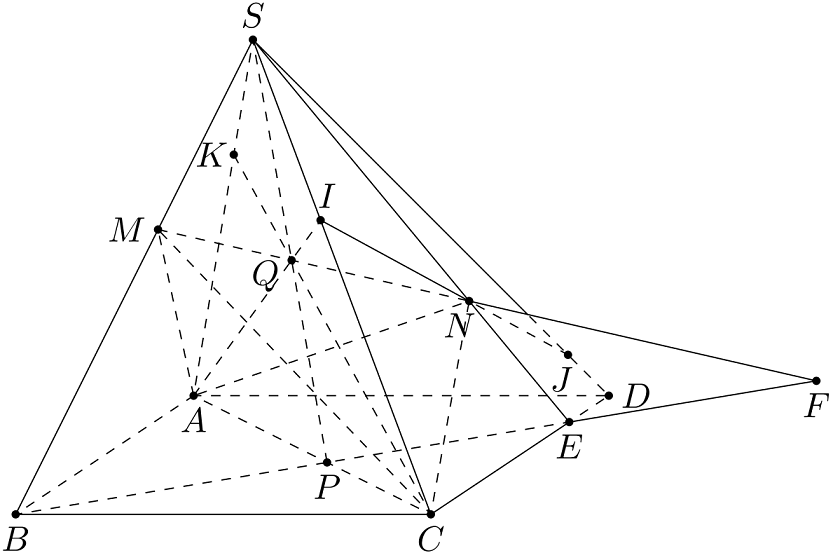
a) Trong $(SCD)$, gọi $E=SN\cap CD$.
Trong $(SBE)$, gọi $F=MN\cap BE$.
Ta có $\begin{cases}F\in BE,\,BE\subset(ABCD)\Rightarrow F\in(ABCD)\\ F\in MN\end{cases}$
Suy ra $F=MN\cap(ABCD)$.

b) Trong $(ABCD)$, gọi $P=BE\cap AC$. Vì $P\in BE$, $BE\subset(SBE)$ nên $P\in(SBE)$.
Trong $(SBE)$, gọi $Q=SP\cap MN$. Vì $Q\in SP$, $SP\subset(SAC)$ nên $Q\in(SAC)$.

Trong $(SAC)$, gọi $I=AQ\cap SC$.
Ta có $\begin{cases}I\in AQ,\,AQ\subset(AMN)\Rightarrow I\in(AMN)\\ I\in SC\end{cases}$
Suy ra $I=SC\cap(AMN)$.

c) Trong $(SCD)$, gọi $J=IN\cap SD$.
Ta có $\begin{cases}J\in IN,\,IN\subset(AMN)\Rightarrow J\in(AMN)\\ J\in SD\end{cases}$
Suy ra $J=SD\cap(AMN)$.

d) Trong $(SAC)$, gọi $K=CQ\cap SA$.
Ta có $\begin{cases}K\in CQ,\,CQ\subset(CMN)\Rightarrow K\in(CMN)\\ K\in SA\end{cases}$
Suy ra $K=SA\cap(CMN)$.