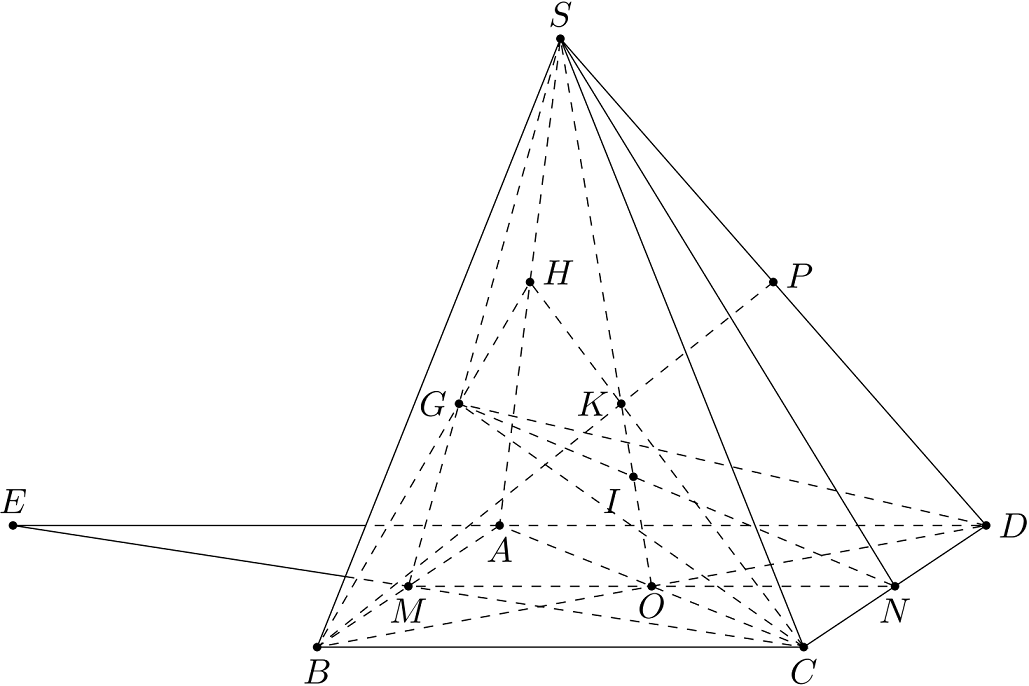
a) Trong $(SAB)$, gọi $M=SG\cap AB$.
Ta có $\begin{cases}M\in SG,\,SG\subset(SGC)\Rightarrow M\in(SGC)\\ M\in AB,\,AB\subset(ABCD)\Rightarrow M\in(ABCD)\end{cases}$
Suy ra $M\in(SGC)\cap(ABCD)$.

Mặt khác $C\in(SGC)\cap(ABCD)$. Do đó $(SGC)\cap(ABCD)=MC$.

b) Trong $(ABCD)$, gọi $E=MC\cap AD$.
Ta có $\begin{cases}E\in MC,\,MC\subset(SGC)\Rightarrow E\in(SGC)\\ E\in AD\end{cases}$
Suy ra $E=AD\cap(SGC)$.

c) Trong $(ABCD)$, gọi $N=OM\cap CD$. Vì $CD\subset(GCD)$ nên $N\in(GCD)$.

Trong $(SMN)$, gọi $I=SO\cap GN$.
Ta có $\begin{cases}I\in GN,\,GN\subset(GCD)\Rightarrow I\in(GCD)\\ I\in SO\end{cases}$
Suy ra $I=SO\cap(GCD)$.

d) Trong $(SAB)$, gọi $H=BG\cap SA$. Vì $H\in SA$, $SA\subset(SAC)$ nên $H\in(SAC)$.

Trong $(SAC)$, gọi $K=CH\cap SO$. Vì $K\in SO$, $SO\subset(SBD)$ nên $K\in(SBD)$.

Trong $(SBD)$, gọi $P=BK\cap SD$.

Ta có $H\in BG$, $BG\subset(BCG)\Rightarrow H\in(BCG)\Rightarrow CH\subset(BCG)$, mà $K\in CH$ nên $K\in(BCG)$.
Do đó $\begin{cases}P\in BK,\,BK\subset(BCG)\Rightarrow P\in(BCG)\\ P\in SD\end{cases}$
Suy ra $P=SD\cap(BCG)$.