Ngân hàng bài tập
A
Cho lăng trụ $ABC.A'B'C'$ có đáy $ABC$ là tam giác đều cạnh bằng $2a$. Hình chiếu vuông góc của $A'$ lên mặt phẳng $(ABC)$ trùng với trung điểm $H$ của cạnh $BC$ và $A'H=a\sqrt{3}$. Tính theo $a$ thể tích $V$ của khối lăng trụ $ABC.A'B'C'$.
| $V=3a^3$ | |
| $V=a^3$ | |
| $V=\dfrac{3a^3}{4}$ | |
| $V=\dfrac{3a^3}{2}$ |
1 lời giải
Chọn phương án A.
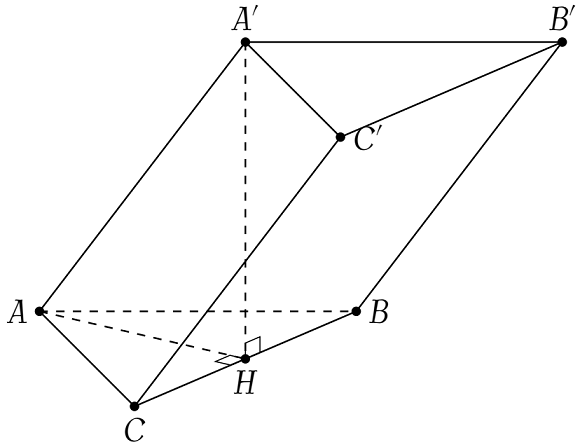
Diện tích tam giác $ABC$ là $$S_{ABC}=\dfrac{(2a)^2\sqrt{3}}{4}=a^2\sqrt{3}$$
Vì $H$ là hình chiếu vuông góc của $A'$ trên $(ABC)$ nên $A'H$ vuông góc $(ABC)$ hay $A'H$ là đường cao của lăng trụ $ABC.A'B'C'$.
Thể tích của khối lăng trụ $ABC.A'B'C'$ là $$V=S_{ABC}\cdot A'H=a^2\sqrt{3}\cdot a\sqrt{3}=3a^3.$$
