Cho hình chóp tam giác $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $2a$ và $SA$ vuông góc với mặt phẳng $(ABC)$ (tham khảo hình vẽ).
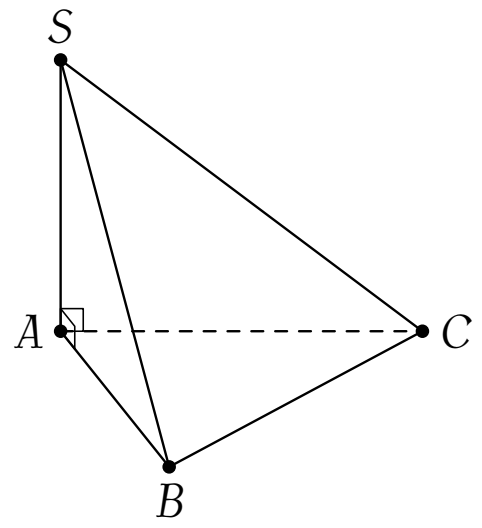
Biết thể tích của khối chóp $S.ABC$ là $\dfrac{a^3\sqrt{3}}{2}$ và góc giữa hai mặt phẳng $(SBC)$ và $(ABC)$ là góc nhọn $\alpha$. Chọn phát biểu đúng.
| $\alpha=60^{\circ}$ | |
| $\alpha=45^{\circ}$ | |
| $\alpha=30^{\circ}$ | |
| $\tan\alpha=\dfrac{\sqrt{3}}{2}$ |
Chọn phương án D.
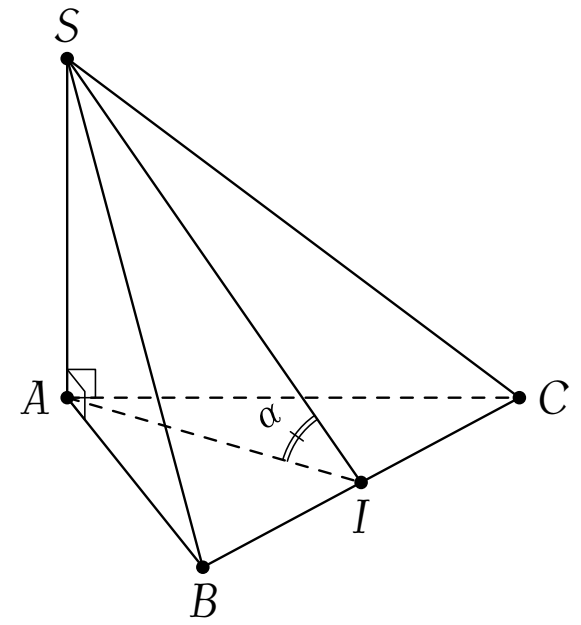
Tam giác $ABC$ đều $\Rightarrow S_{ABC}=(2a)^2\cdot\dfrac{\sqrt{3}}{4}=a^2\sqrt{3}$.
Ta có $V_{S.ABC}=\dfrac{1}{3}S_{ABC}\cdot SA$
Suy ra $SA=\dfrac{3V_{S.ABC}}{S_{ABC}}=\dfrac{3\cdot\dfrac{a^3\sqrt{3}}{2} }{a^2\sqrt{3}}=\dfrac{3a}{2}$.
Gọi $I$ là trung điểm của $BC$.
Do tam giác $ABC$ đều nên $AI\perp BC$.
Ta lại có $SA\perp BC$ suy ra $BC\perp \left(SAI\right)\Rightarrow SI\bot BC$.
Vậy $\alpha=\left((SBC),(ABC)\right)=\widehat{SIA}$.
Xét tam giác vuông $SAI$ ta có $$\tan\alpha=\dfrac{SA}{AI}=\dfrac{\dfrac{3a}{2}}{a\sqrt{3}}=\dfrac{\sqrt{3}}{2}.$$
