Ngân hàng bài tập
A
Cho tứ diện $ABCD$. Các điểm $M$, $N$, $P$ lần lượt thuộc các cạnh $AB$, $AC$, $AD$ sao cho $MA=MB$, $NA=2NC$, $PA=3PD$. Biết thể tích khối tứ diện $AMNP$ bằng $V$ thì khối tứ diện $ABCD$ tính theo $V$ có giá trị là
| $4V$ | |
| $6V$ | |
| $12V$ | |
| $8V$ |
1 lời giải
Chọn phương án A.
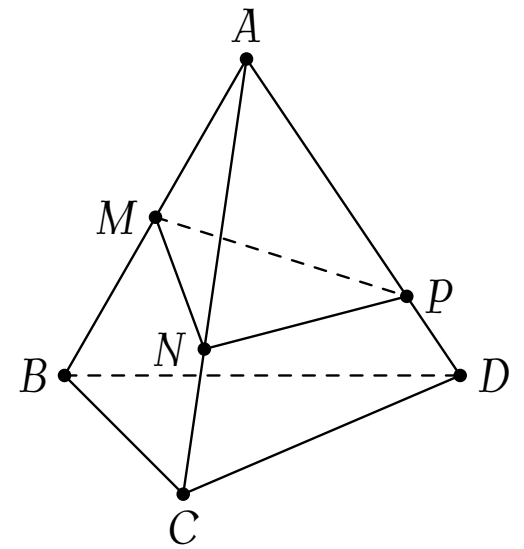
Ta có $\dfrac{V_{AMNP}}{V_{ABCD}}=\dfrac{AM}{AB}\cdot\dfrac{AN}{AC}\cdot\dfrac{AP}{AD}=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot\dfrac{3}{4}=\dfrac{1}{4}$.
$\Rightarrow V_{ABCD}=4V_{AMNP}=4V$.
