Ngân hàng bài tập
S
Cho khối chóp $S.ABCD$ có đáy là hình bình hành và có thể tích $48$. Trên các cạnh $SA,\,SB,\,SC,\,SD$ lần lượt lấy các điểm $A',\,B',\,C'$ và $D'$ sao cho $\dfrac{SA'}{SA}=\dfrac{SC'}{SC}=\dfrac{1}{3}$ và $\dfrac{SB'}{SB}=\dfrac{SD'}{SD}=\dfrac{3}{4}$. Tính thể tích $V$ của khối đa diện lõm $S.A'B'C'D'$.
| $V=4$ | |
| $V=9$ | |
| $V=\dfrac{3}{2}$ | |
| $V=6$ |
1 lời giải
Chọn phương án A.
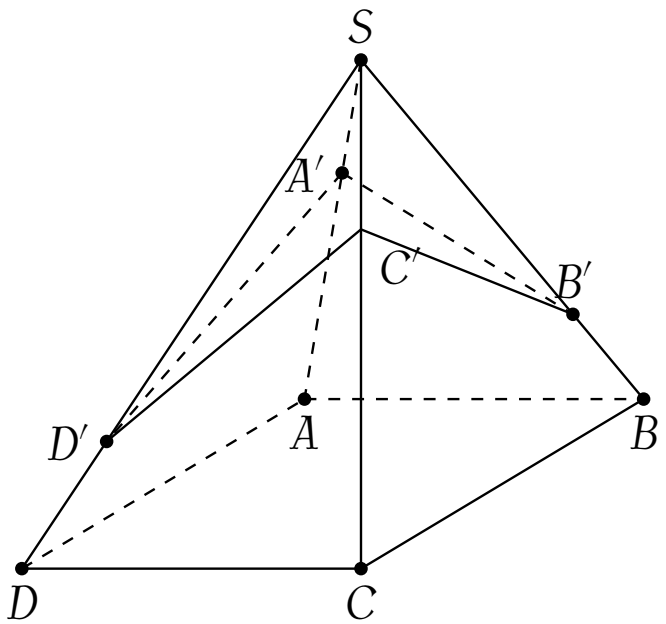
Ta có $\dfrac{V_{S.A'B'C'}}{V_{S.ABC}}=\dfrac{SA'}{SA}\cdot \dfrac{SB'}{SB}\cdot\dfrac{SC'}{SC}=\dfrac{1}{3}\cdot\dfrac{3}{4}\cdot\dfrac{1}{3}=\dfrac{1}{12}$.
$\Rightarrow V_{S.A'B'C'}=\dfrac{1}{12}\cdot V_{S.ABC}=\dfrac{1}{12}\cdot\dfrac{48}{2}=2$.
Tương tự $V_{S.A'D'C'}=2$.
Suy ra thể tích cần tính là $$V_{S.A'B'C'D'}=V_{S.A'B'C'}+V_{S.A'D'C'}=4.$$
