Ngân hàng bài tập
A
Trong không gian \(Oxyz\), cho điểm \(I(-3;0;1)\). Mặt cầu \((S)\) có tâm \(I\) và cắt mặt phẳng \((P)\colon x-2y-2z-1=0\) theo một thiết diện là hình tròn. Biết rằng diện tích của hình tròn này bằng \(\pi\). Phương trình mặt cầu \((S)\) là
| \((x+3)^2+y^2+(z-1)^2=4\) | |
| \((x+3)^2+y^2+(z-1)^2=25\) | |
| \((x+3)^2+y^2+(z-1)^2=5\) | |
| \((x+3)^2+y^2+(z-1)^2=2\) |
1 lời giải
Chọn phương án C.
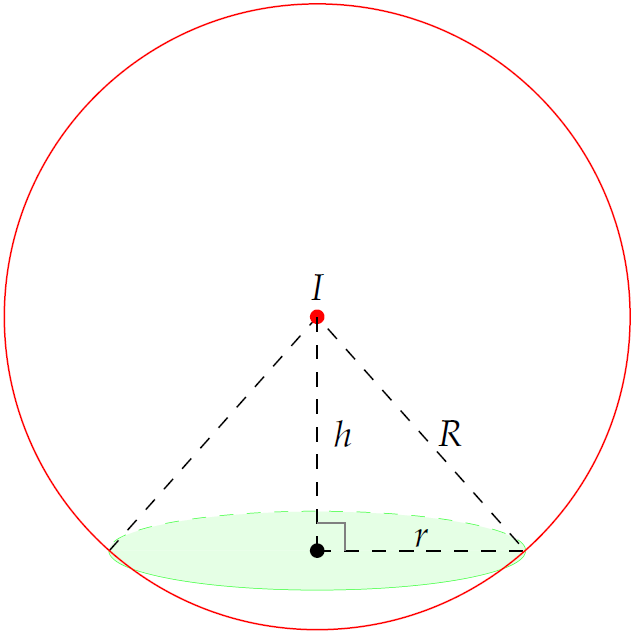
Gọi \(R\) và \(r\) lần lượt là bán kính của mặt cầu \((S)\) và hình tròn thiết diện, \(h\) là khoảng cách từ \(I\) đến mặt phẳng \((P)\). Ta có:
- \(\pi\cdot r^2=\pi\Leftrightarrow r=1\).
- \(h=d\left(I,(P)\right)=2\)
- \(R^2=r^2+h^2=1^2+2^2=5\).
Khi đó, \((S)\colon(x+3)^2+y^2+(z-1)^2=5\).
