Ngân hàng bài tập
A
Trong không gian \(Oxyz\), cho mặt cầu \((S)\colon(x-1)^2+(y-1)^2+(z-1)^2=25\) có tâm \(I\) và mặt phẳng \((P)\colon x+2y+2z+7=0\). Thể tích của khối nón có đỉnh \(I\) và đáy là giao tuyến của mặt cầu \((S)\) và mặt phẳng \((P)\) bằng
| \(12\pi\) | |
| \(48\pi\) | |
| \(36\pi\) | |
| \(24\pi\) |
1 lời giải
Chọn phương án A.
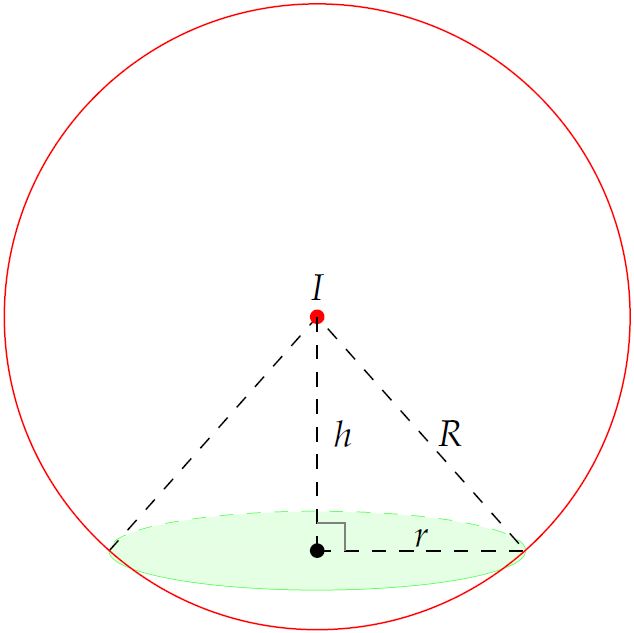
Mặt cầu \((S)\) có tâm \(I(1;1;1)\) và bán kính \(R=5\).
Gọi \(h\) là khoảng cách từ tâm \(I\) đến mặt phẳng \((P)\) và \(r\) là bán kính đáy của hình nón. Ta có:
- \(h=d\left(I,(P)\right)=4\).
- \(r^2=R^2-h^2=25-16=9\).
Vậy thể tích khối nón bằng $$V=\dfrac{1}{3}\pi r^2 h=\dfrac{1}{3}\pi\cdot9\cdot4=12\pi$$
