Ngân hàng bài tập
Gieo một con súc sắc cân đối và đồng chất. Giả sử súc sắc xuất hiện mặt \(b\) chấm. Tính xác suất để phương trình \(x^2+bx+2=0\) có hai nghiệm phân biệt.
1 lời giải
Ta có \(n\left(\Omega\right)=6\).
Phương trình \(x^2+bx+2=0\) có hai nghiệm phân biệt khi và chỉ khi \(\Delta=b^2-8>0\).
Bảng xét dấu:
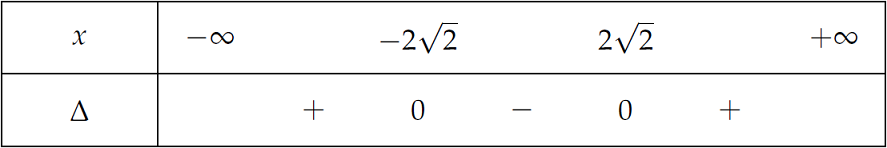

Suy ra \(b\in(-\infty;-2\sqrt{2})\cup(2\sqrt{2};+\infty)\).
Vì \(b\) là số chấm xuất hiện trên súc sắc nên \(b\in\{3;4;5;6\}\).
Vậy xác suất cần tìm là $$P=\dfrac{4}{6}=\dfrac{2}{3}.$$
