Cho hình chóp \(S.ABC\) có đáy là tam giác đều cạnh \(a\), cạnh bên \(SA=2a\) và vuông góc với mặt đáy. Gọi \(M,\,N\) lần lượt là hình chiếu vuông góc của \(A\) trên các đường thẳng \(SB\), \(SC\).
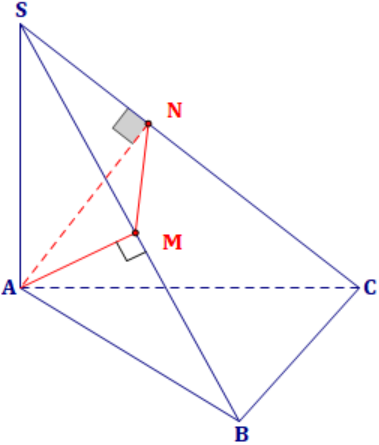
Tính thể tích của khối chóp \(A.BCNM\).
Ta có $$\begin{align*}
V_{S.ABC}&=V_{S.AMN}+V_{A.BCNM}\\
\Rightarrow V_{A.BCNM}&=V_{S.ABC}-V_{S.AMN}
\end{align*}$$
- \(S_{ABC}=\dfrac{a^2\sqrt{3}}{4}\)
- Đường cao \(SA=2a\)
\(\Rightarrow V_{S.ABC}=\dfrac{1}{3}\cdot\dfrac{a^2\sqrt{3}}{4}\cdot2a=\dfrac{a^3\sqrt{3}}{6}\)
Ta có tỷ số $$\dfrac{V_{S.AMN}}{V_{S.ABC}}=\dfrac{SA}{SA}\cdot\dfrac{SM}{SB}\cdot\dfrac{SN}{SC}=\dfrac{SM}{SB}\cdot\dfrac{SN}{SC}$$
- \(SB^2=SA^2+AB^2=5a^2\)
- \(AM\) là đường cao \(\Rightarrow SM\cdot SB=SA^2\)
\(\Rightarrow\dfrac{SM}{SB}=\dfrac{SA^2}{SB^2}=\dfrac{4a^2}{5a^2}=\dfrac{4}{5}\)
♥ Xét tam giác vuông \(SAC\) ta có
- \(SC^2=SA^2+AC^2=5a^2\)
- \(AN\) là đường cao \(\Rightarrow SN\cdot SC=SA^2\)
\(\Rightarrow\dfrac{SN}{SC}=\dfrac{SA^2}{SC^2}=\dfrac{4a^2}{5a^2}=\dfrac{4}{5}\)
Do đó \(\dfrac{V_{S.AMN}}{V_{S.ABC}}=\dfrac{4}{5}\cdot\dfrac{4}{5}=\dfrac{16}{25}\)
\(\begin{align*}
\Rightarrow V_{S.AMN}&=\dfrac{16}{25}V_{S.ABC}\\
&=\dfrac{16}{25}\cdot\dfrac{a^3\sqrt{3}}{6}\\
&=\dfrac{8a^3\sqrt{3}}{75}
\end{align*}\)
\(\begin{align*}
\Rightarrow V_{A.BCNM}&=V_{S.ABC}-V_{S.AMN}\\
&=\dfrac{a^3\sqrt{3}}{6}-\dfrac{8a^3\sqrt{3}}{75}\\
&=\dfrac{3a^3\sqrt{3}}{50}
\end{align*}\)
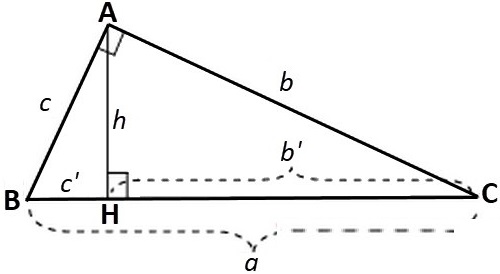
Khi đó:
- \(b^2=a\cdot b'\)
- \(c^2=a\cdot c'\)