Cho \(\displaystyle\int\limits^5_1\left|\dfrac{x-2}{x+1}\right| \mathrm{\,d}x=a\ln3+b\ln2+c\) với \(a,\,b,\,c\) là các số nguyên. Giá trị \(P=abc\) là
| \(P=-36\) | |
| \(P=0\) | |
| \(P=18\) | |
| \(P=-18\) |
Chọn phương án A.
Đặt $A=\displaystyle\int\limits^5_1\left|\dfrac{x-2}{x+1}\right| \mathrm{\,d}x$ ta có $$A-c=\ln3^a2^b\Leftrightarrow\mathrm{e}^{A-c}=3^a2^b$$Vì $a,\,b,\,c\in\mathbb{Z}$ nên ta khảo sát hàm số $f(x)=\mathrm{e}^{A-x}$ với $x\in\mathbb{Z}$ bằng chức năng TABLE của máy tính cầm tay.
- Gán giá trị $\displaystyle\int\limits^5_1\left|\dfrac{x-2}{x+1}\right| \mathrm{\,d}x$ vào biến nhớ A.

- Nhập hàm số $f(x)=\mathrm{e}^{A-x}$.

- Chọn Start=-10, End=10 và Step=1.
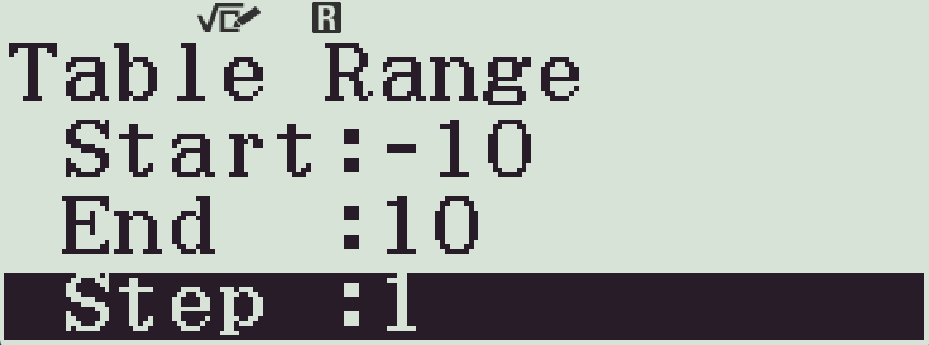
- Ta tìm giá trị $f(x)\in\mathbb{Q}$.

Ta biết $\dfrac{27}{64}=27\cdot\dfrac{1}{64}=3^3\cdot2^{-6}$. Suy ra $a=3$ và $b=-6$, đồng thời $c=2$.
Vậy $abc=3\cdot(-6)\cdot2=-36$.
Chọn phương án A.
Ta thấy: $$\left|\dfrac{x-2}{x+1}\right|=\begin{cases}\dfrac{x-2}{x+1} &\text{khi }x<-1\text{ hoặc }x\geq2\\ \dfrac{2-x}{x+1} &\text{khi }-1< x<2.\end{cases}$$
Do đó: $$\begin{eqnarray*}
&&\displaystyle\int\limits^5_1\left|\dfrac{x-2}{x+1}\right|\mathrm{\,d}x\\
&=&\displaystyle\int\limits^2_1\dfrac{2-x}{x+1}\mathrm{\,d}x+\int\limits^5_2\dfrac{x-2}{x+1}\mathrm{\,d}x\\
&=&\displaystyle\int\limits_1^2\left(\dfrac{3}{x+1}-1\right)\mathrm{\,d}x+\displaystyle\int\limits_2^5\left(1-\dfrac{3}{x+1}\right)\mathrm{\,d}x\\
&=&\left(3\ln|x+1|-x\right)\bigg|_1^2+\left(x-3\ln|x+1|\right)\bigg|_2^5\\
&=&2+3\ln3-6\ln2.\end{eqnarray*}$$
Theo đó \(a=3,\,b=-6,\,c=2\Rightarrow P=-36\).
