Ngân hàng bài tập
S
Cho hàm bậc bốn $y=f(x)$ có đồ thị $f'(x)$ như hình vẽ bên.
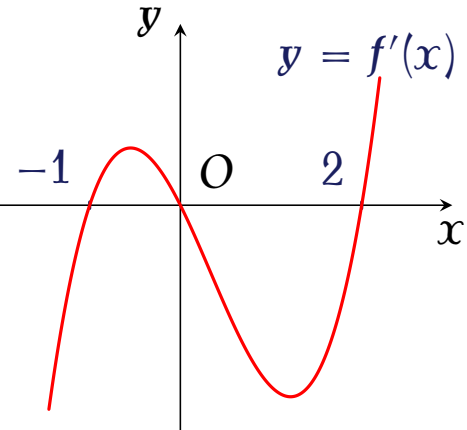
Hàm số $y=f(1-3x)-4$ nghịch biến trên khoảng
| $\left(-\dfrac{1}{3};\dfrac{1}{3}\right)$ | |
| $(0;2)$ | |
| $(-\infty;-1)$ | |
| $\left(\dfrac{1}{3};\dfrac{2}{3}\right)$ |
1 lời giải
Chọn phương án D.
Ta có $y'=-3f'(1-3x)$. Khi đó $$\begin{aligned}
y'<0&\Leftrightarrow-3f'(1-3x)<0\\
&\Leftrightarrow f'(1-3x)>0\\
&\Leftrightarrow\left[\begin{array}{l}-1<1-3x<0\\ 1-3x>2\end{array}\right.\Leftrightarrow\left[\begin{array}{l}\dfrac{1}{3}<x<\dfrac{2}{3}\\ x<-\dfrac{1}{3}.\end{array}\right.
\end{aligned}$$
Vậy hàm số $y=f(1-3x)-4$ nghịch biến trên khoảng $\left(\dfrac{1}{3};\dfrac{2}{3}\right)$ và $\left(-\infty;-\dfrac{1}{3}\right)$.
