Ngân hàng bài tập
S
Cho hàm số $f$ có đạo hàm liên tục trên $(-1;3)$. Bảng biến thiên của hàm số $f'(x)$ như hình vẽ.
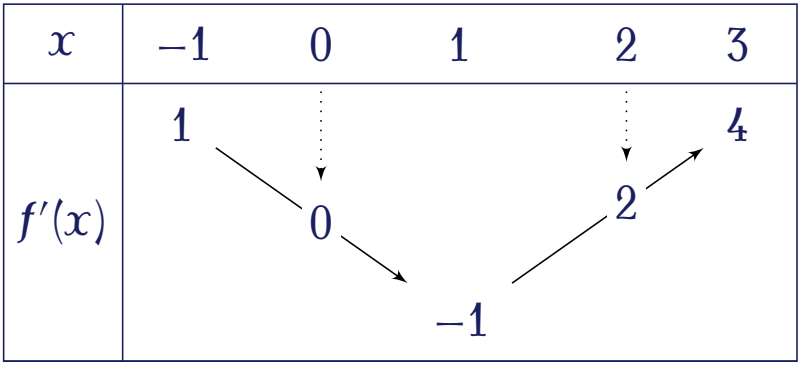
Hàm số $g(x)=f\left(1-\dfrac{x}{2}\right)+x$ nghịch biến trên khoảng nào trong các khoảng sau?
| $(-4;-2)$ | |
| $(2;4)$ | |
| $(-2;0)$ | |
| $(0;2)$ |
1 lời giải
Chọn phương án A.
Ta có $g'(x)=-\dfrac{1}{2}f'\left(1-\dfrac{x}{2}\right)+1$.
Xét $\begin{aligned}[t]
g'(x)\leq0&\Leftrightarrow-\dfrac{1}{2}f'\left(1-\dfrac{x}{2}\right)+1\leq0\\
&\Leftrightarrow f'\left(1-\dfrac{x}{2}\right)\geq2\\
&\Leftrightarrow2\leq1-\dfrac{x}{2}\leq3\\
&\Leftrightarrow1\leq-\dfrac{x}{2}\leq2\\
&\Leftrightarrow2\leq-x\leq4\\
&\Leftrightarrow-4\geq x\geq-2.
\end{aligned}$
Do đó hàm số nghịch biến trên khoảng $(-4;-2)$.
