Ngân hàng bài tập
SS
Cho hàm số $f(x)$ có đạo hàm liên tục trên $\mathbb{R}$. Đồ thị hàm số $f'(x)$ được cho như hình vẽ.
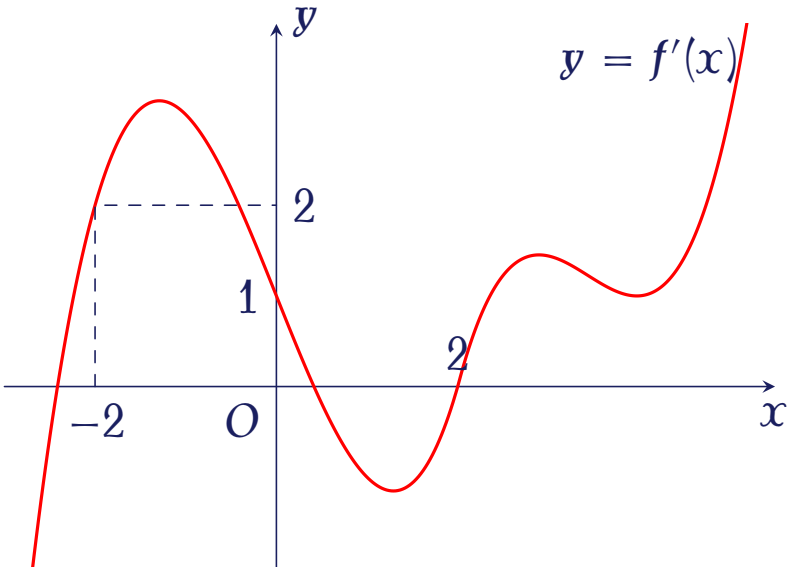
Hàm số $g(x)=4f(x)+x^2-4x+2022$ đồng biến trên khoảng nào sau đây?
| $[-2;0]$ và $[2;+\infty)$ | |
| $(-\infty;-2]$ và $[0;2]$ | |
| $[-2;2]$ | |
| $(-\infty;-2]$ và $[2;+\infty)$ |
1 lời giải
Chọn phương án A.
Ta có $g'(x)=4f'(x)+2x-4=4\left[f'(x)-\left(1-\dfrac{x}{2}\right)\right]$.
Để hàm số đồng biến thì $$g'(x)\geq0\Leftrightarrow f'(x)-\left(1-\dfrac{x}{2}\right)\geq0\Leftrightarrow f'(x)\geq1-\dfrac{x}{2}$$
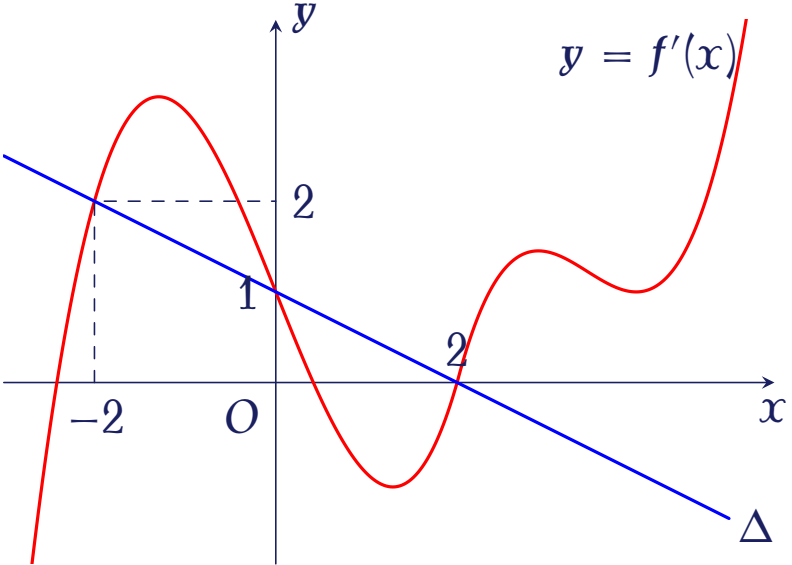
Dựa vào đồ thị ta thấy đồ thị $f'(x)$ nằm phía trên so với đường thẳng $\Delta\colon y=1-\dfrac{x}{2}$ trên khoảng $[-2;0]$ và $[2;+\infty)$.
Vậy hàm số $g(x)$ đồng biến trên các khoảng $[-2;0]$ và $[2;+\infty)$.
