Ngân hàng bài tập
S
Tìm tập hợp giá trị của tham số $m$ để hàm số $y=x^3-mx^2-(m-6)x+1$ đồng biến trên khoảng $(0;4)$.
| $(-\infty;6]$ | |
| $(-\infty;3]$ | |
| $(-\infty;3)$ | |
| $[3;6]$ |
1 lời giải
Chọn phương án B.
Ta có $y'=3x^2-2mx-m+6$. Để hàm số đồng biến trên khoảng $(0;4)$ thì $$\begin{aligned}
y'\geq0,\,\forall x\in(0;4)&\Leftrightarrow3x^2-2mx-m+6\geq0,\,\forall x\in(0;4)\\
&\Leftrightarrow3x^2+6-m(2x+1)\geq0,\,\forall x\in(0;4)\\
&\Leftrightarrow m\leq\dfrac{3x^2+6}{2x+1},\,\forall x\in(0;4).
\end{aligned}$$
Xét hàm số $g(x)=\dfrac{3x^2+6}{2x+1}$ trên khoảng $(0;4)$.
Ta có $g'(x)=\dfrac{6x^2+6x-12}{(2x+1)^2}$.
Cho $g'(x)=0\Leftrightarrow6x^2+6x-12=0\Leftrightarrow\left[\begin{array}{ll}x=1 &\in(0;4)\\ x=-2&\notin(0;4)\end{array}\right.$
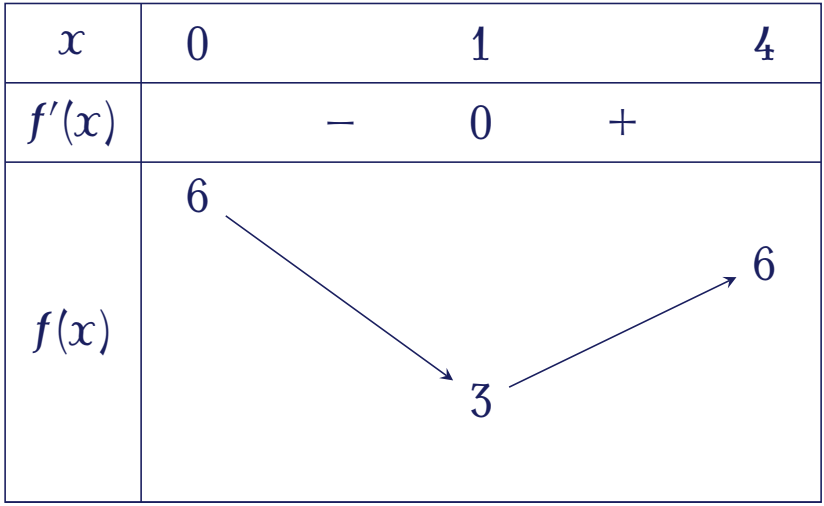
Vậy $m\leq\dfrac{3x^2+6}{2x+1},\,\forall x\in(0;4)\Leftrightarrow m\leq3$.
