Ngân hàng bài tập
SS
Cho hàm số $y=f(x)$ có đạo hàm trên $\mathbb{R}$ và có đồ thị hàm $f'(x)$ như hình vẽ.
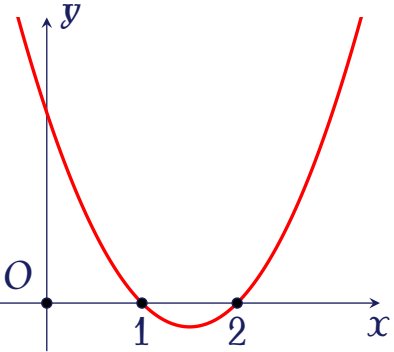
Tìm khoảng nghịch biến của hàm số $g(x)=f\big(x-x^2\big)$.
| $\left(-\dfrac{1}{2};+\infty\right)$ | |
| $\left(-\dfrac{3}{2};+\infty\right)$ | |
| $\left(-\infty;\dfrac{3}{2}\right)$ | |
| $\left(\dfrac{1}{2};+\infty\right)$ |
1 lời giải
Chọn phương án D.
Ta có $g'(x)=(1-2x)f'\big(x-x^2\big)$.
Cho $g'(x)=0\Leftrightarrow\left[\begin{array}{l}1-2x=0\\ f'\big(x-x^2\big)=0\end{array}\right.\Leftrightarrow\left[\begin{array}{ll}x=\dfrac{1}{2}\\ x-x^2=1 &(\text{vô nghiệm})\\ x-x^2=2 &(\text{vô nghiệm})\end{array}\right.$

Dựa vào bảng xét dấu ta thấy $g(x)$ nghịch biến trên khoảng $\left(\dfrac{1}{2};+\infty\right)$.
